W tym zadaniu musisz wyliczyć jak długa jest wysokość trójkąta opuszczona z wierzchołka A, jeśli trójkąt ten jest wyznaczony przez wierzchołki A = (1, 4), B = (-3, -2) i C = (5, 2). Wylicz także jakie pole ma ten trójkąt.
![]()
Więc wysokość opuszczona z wierzchołka A, to odległość punktu A od prostej zawierającej bok BC (prosta ta będzie oznaczana jako BC)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
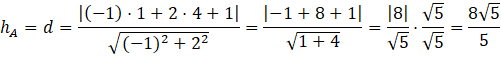
Pole trójkąta ABC, obliczane przy użyciu wysokości hA to:
![]()
![]()
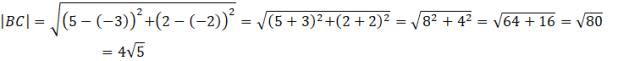
![]()

Wysokość, jest to odcinek prostopadły do boku. Zauważ, że obliczenie długości wysokości będzie tożsame z obliczeniem odległości punktu A od prostej zawierającej przeciwległy bok, czyli BC. Niech ta prosta także nazywa się prostą BC.
Prosta BC, przechodzi przez punkty B oraz C. Więc jej współczynnik kierunkowy możesz wyliczyć, ze wzoru na współczynnik kierunkowy prostej przechodzącej przez punkty (x1, y1) oraz (x2, y2).
![]()
Podstawiając odpowiednio współrzędne B i C otrzymasz wynik:
![]()
Pamiętaj, że co prawda kolejność uwzględnianych punktów jest dowolna, ale musi być taka sama dla x-ów i y-ów. Więc jeśli przyjmiesz, że punktem o współrzędnych (x2, y2) jest punkt B, to musisz konsekwentnie podstawiać za y2 i x2 współrzędne punktu B.
Równanie prostej BC możesz na chwilę obecną zapisać jako:
![]()
Prosta BC przechodzi, przez punkty B oraz C, więc podstawiając do równania kierunkowego prostej BC za x pierwszą współrzędną któregoś z tych punktów, powinieneś otrzymać w wyniku drugą współrzędną. W tym przypadku wybrany został punkt C.
![]()
![]()
![]()
Więc prosta BC zawierająca bok BC wyraża się wzorem:
![]()
Aby obliczyć odległość punktu A od prostej BC, czyli wysokość opuszczoną z wierzchołka A musisz skorzystać ze wzoru na odległość punktu o współrzędnych (x0, y0) od prostej o równaniu Ax + By + C = 0. Wzór ten to:
![]()
Jednakże prosta którą wyznaczyłeś jest w postaci kierunkowej, więc musisz zamienić jej równanie na postać ogólną.
Spójrz, jak wygląda postać ogólna równania prostej. Po jednej stronie równania jest 0, zaś po drugie wyrażenia z x, y oraz wyraz wolny. Więc aby sprowadzić podane równania do postaci ogólnej musisz przenieść wszystkie składniki na jedną stronę. Dobrze jest także pozbyć się ewentualnych ułamków, przez przemnożenie obu stron przez ich mianowniki.
![]()
![]()
![]()
Teraz wystarczy, że odczytasz poszczególne współczynniki z równania, i podstawisz je do wzoru, razem z współrzędnymi punktu A.
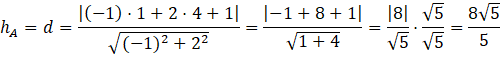
Oczywiście, ponieważ w mianowniku pojawił się pierwiastek, musisz usunąć niewymierność z mianownika, przez przemnożenie zarówno licznika jak i mianownika przez ten pierwiastek.
Pole trójkąta to:
![]()
Gdzie a to bok trójkąta, a ha to wysokość opuszczona na niego. W rozważanym trójkącie wzór ten będzie miał postać:
![]()
Gdyż obliczona wysokość hA jest opuszczona na bok BC. Musisz więc obliczyć długość boku BC. Skorzystaj ze wzoru na długość odcinka łączącego dwa punkty.
![]()
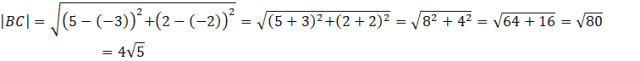
Podstawiając do wzoru na pole trójkąta otrzymasz:
![]()

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
