W tym zadaniu trzeba ustalić jakie równanie będą miały proste które są prostopadłe względem prostej opisanej jako y = 2x oraz styczne z okręgiem opisanym równaniem: x² + y² = 1.

k – szukana prosta

l – prosta podana w treści zadania

$\text{[math]}$

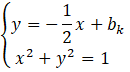
Ponieważ prosta styczna do okręgu ma tylko jeden punkt wspólny z tym okręgiem, więc powyższe równanie musi mieć jedno rozwiązanie. Ponieważ jest to równanie kwadratowe, to jedno rozwiązanie ma wtedy i tylko wtedy, gdy:

$\text{[math]}$

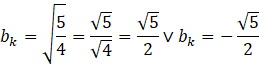
Równania prostych równoległych do prostej podanej w treści zadania i stycznych do podanego okręgu to:

$\text{[math]}$

Współczynniki kierunkowe prostych prostopadłych do siebie spełniają warunek:

$\text{[math]}$

Więc aby obliczyć współczynnik kierunkowy szukanej prostej musisz do tego wzoru podstawić współczynnik podanej prostej.

$\text{[math]}$

Możesz zapisać, że szukana prosta jest zadana równaniem (oznacz ją jako k):

$\text{[math]}$

Punkt styczności będzie należał zarówno do szukanej prostej, jak i do podanego okręgu. Więc jego współrzędne będą spełniań oba równania na raz. Jednakże, równanie takie musi mieć jedno rozwiązane, gdyż dla jednej prostej stycznej do okręgu, jest tylko jeden punkt, który należy do obu. Gdyby były dwa takie punkty, to prosta przecinałaby okrąg, a nie byłaby styczna. Zapisz oba równania jako układ równań:

$\text{[math]}$

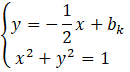
Zauważ, że z równania prostej masz od razu wyznaczoną zmienną y w zależności od x oraz b_k. Aby uzyskać równanie z jedną zmienną wystarczy, że do równania okręgu za y podstawisz równanie prostej.

$\text{[math]}$

Nawias wylicz ze wzoru skróconego mnożenia

$\text{[math]}$

A następnie uprość wyrażenie i przenieś wszystkie składniki na jedną stronę. Warto także zapisać to jako równanie ze względu na x, a więc uporządkuj je tak, by wszystkie składniki z x były obok siebie.

$\text{[math]}$

Zauważ, że otrzymałeś równanie kwadratowe ze względu na x. Równanie to powinno mieć tylko jedno rozwiązanie (jedną wartość x będącego pierwszą współrzędną punktu styczności). Równanie kwadratowe ma jedno rozwiązanie tylko wtedy, gdy Δ = 0. Więc musisz obliczyć Δ i przyrównać ją do zera.

$\text{[math]}$

Dostałeś kolejne równanie kwadratowe. Pamiętaj, że jest to osobne równanie niż to które dostałeś z układu równań. Tam, było to równanie ze względu na x i jego rozwiązaniem była jakaś wartość x (czyli pierwszej współrzędnej punktu styczności). Natomiast tutaj zmienną jest b_k i wynikiem będzie wartość właśnie tego współczynnika. Aby otrzymać wynik wystarczy, że rozwiążesz to równanie kwadratowe, przez przeniesienie wyrazu wolnego na drugą stronę.

$\text{[math]}$

Oczywiście musisz pamiętać, że gdy pierwiastkujesz obie strony równania musisz rozważyć dwa przypadki.

$\text{[math]}$

Otrzymałeś dwie wartości współczynnika b_k, co oznacza, że istnieją dwie proste styczne do podanego okręgu i równoległe do podanej w treści zadania prostej. Znając współczynnik b_k możesz zapisać ich równania.

$\text{[math]}$