W tym zadaniu musisz wyliczyć wartość kąta ostrego pod którym prosta zadana równaniem 2x + 3y + 15 = 0 przecina się z prostą o równaniu 5x – 2y – 10 = 0. Dozwolone jest użycie tablic trygonometrycznych lub kalkulatora.

$\text{[math]}$

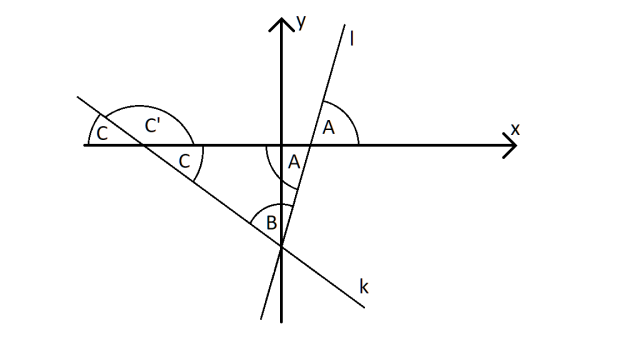
Kąty A i C to kąty między osią OX a odpowiednio prostymi k i l

$\text{[math]}$

Kąt A – kąt ostry

$\text{[math]}$

C’ – kąt przyległy do kąta C

$\text{[math]}$

Odp.: Podane proste przecinają się pod kątem ok. 78°.

Dla łatwiejszego zapisu przyjmij, że prosta o równaniu 2x + 3y + 15 = 0 to prosta k, zaś prosta 5x – 2y – 10 = 0 to prosta l. Dobrze jest sporządzić rysunek pomocniczy, aby można było coś łatwiej zauważyć. Oczywiście nie musi to być dokładny rysunek, jednak musisz zachować podstawowe własności tych prostych. Proste łatwiej jest narysować, gdy podane są w postaci kierunkowej. Dlatego warto zamienić obie proste na postacie kierunkowe.

$\text{[math]}$

Z własności funkcji liniowej przypomnij sobie, że o tym czy prosta jest rosnąca czy malejąca decyduje znak współczynnika przy x (funkcja liniowa to równanie prostej w postaci kierunkowej). Więc prosta k będzie malejąca (bo przy x stoi ujemny współczynnik), zaś prosta l będzie rosnąca (bo przy x stoi dodatni współczynnik). Musisz też rysując te proste umieścić je w dobrych „miejscach” w układzie współrzędnych. Aby to zrobić wystarczy, że będziesz wiedział czy dana prosta przecina oś OY nad osią OX czy pod. Aby policzyć współrzędne punktu przecięcia się prostej z osią OY do równania prostej podstawiasz x = 0. Gdy zrobisz takie podstawienie to wyraz z x „zniknie” i zostanie sam wyraz wolny. Więc aby określić w którym punkcie funkcja będzie przecinała oś OY wystarczy, że spojrzysz na sam wyraz wolny. Wyraz wolny to automatycznie druga współrzędna punktu przecięcia się z osią OY. Obie proste mają ten sam wyraz wolny, więc będą się one przecinać zarówno ze sobą jak i z osią OY dla y = -5. Mając te informacje możesz narysować rysunek pomocniczy.

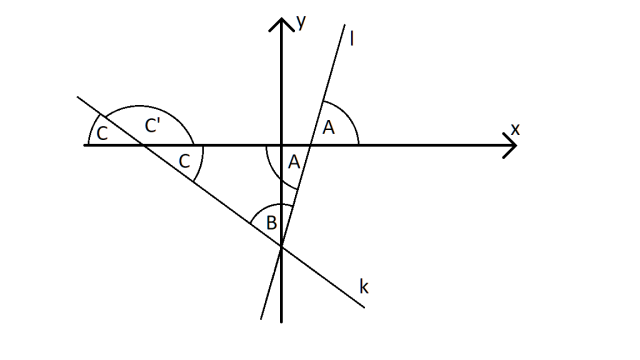
Warto oznaczyć szukane kąty. Zauważ, że ponieważ trójkąt znajduje się „poniżej” osi OX, to szukanych kątów nie otrzymasz wprost z definicji nachylenia prostej do osi OX. Ale zauważ, że kąty te są kątami wierzchołkowymi z kątami z definicji, a więc mają taką samą miarę.

Zauważ, że kąty A i C to kąty między osią OX a odpowiednio prostymi k i l. Przypomnij sobie własność dotyczącą kąta przecięcia się prostej z osią OX. Tangens tego kąta to po prostu współczynnik kierunkowy prostej. A więc dla prostej l zachodzi:

$\text{[math]}$

Oczywiście kąt A jest kątem ostrym (wynika to z samego rysunku, aby kąt A był rozwarty prosta l musiałaby być malejąca). Teraz musisz podać wartość kąta A. Odczytujesz tę wartość albo z tabeli funkcji trygonometrycznych, albo korzystasz z kalkulatora naukowego. Wartość ta wynosi w przybliżeniu:

$\text{[math]}$

W przypadku prostej k zauważ, że gdy postąpisz podobnie, to otrzymasz ten kąt, który jest „na zewnątrz” trójkąta. Jednakże zauważ także, że ten kąt „na zewnątrz” i kąt C, tworzą razem kąty przyległe, a więc ich suma wynosi 180°. Więc, jeśli ten kąt „na zewnątrz” oznaczysz jako C’, to:

$\text{[math]}$

Więc tangens kąta C’ to współczynnik kierunkowy prostej k:

$\text{[math]}$

Teraz zamiast C’ możesz podstawić wyrażenie z C oraz skorzystać ze wzoru redukcyjnego.

$\text{[math]}$

Oczywiście kąt C jest kątem ostrym (wynika to z samego rysunku, aby kąt C był rozwarty prosta k musiałaby być rosnąca). Teraz musisz podać wartość kąta C. Odczytujesz tę wartość albo z tabeli funkcji trygonometrycznych, albo korzystasz z kalkulatora naukowego. Wartość ta wynosi w przybliżeniu:

$\text{[math]}$