W tym zadaniu trzeba wyliczyć jaką długość ma cięciwa okręgu na rysunku poniżej.
Prosta zawierająca cięciwę: y = -3.
Równanie okręgu: x2 + (y + 2)2 = 9
Wyznaczanie punktów przecięcia okręgu i prostej zawierającej cięciwę:
![]()
![]()
![]()
![]()
![]()
![]()
Więc punkty przecięcia rozważanej prostej i okręgu to:
![]()
![]()
Szukana długość cięciwy to odległość między tymi dwoma punktami:
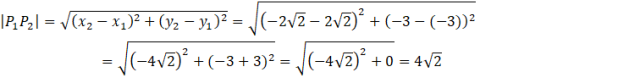

Aby wyznaczyć długość zaznaczonej cięciwy najpierw musisz wyznaczyć punkty przecięcia się prostej zawierającej tę cięciwę z okręgiem, a następnie wyliczyć odległość między tymi punktami. Z kolei, aby wyznaczyć punkty przecięcia się wspomnianej prostej z okręgiem musisz znać równanie tej prostej.
Zauważ, że prosta zawierająca cięciwę jest równoległa do osi OX. Więc jej równanie będzie postaci y = b, gdzie b to pewna liczba. Wszystkie punkty leżące na tej prostej mają drugą współrzędną o wartości -3. Z tego możesz wywnioskować, że równanie tej prostej to y = -3.
Do wyznaczenia punktów przecięcia prostej z okręgiem potrzebujesz także równania okręgu. Aby zapisać równanie okręgu potrzebujesz współrzędnych środka okręgu oraz jego promienia. Obie te wartości musisz odczytać z rysunku. Współrzędne środka tego okręgu to (0, -2), zaś promień wynosi 3. Podstawiając te wartości do równania okręgu otrzymasz, że ten okrąg opisany jest równaniem: x2 + (y + 2)2 = 9 (pamiętaj, że podstawiając do równania współrzędne środka musisz zapisać je z przeciwnym znakiem).
Współrzędne punktów przecięcia podanej prostej z okręgiem będą spełniać układ równań składający się z równań podanej prostej i okręgu. Mają być to punkty, które jednocześnie należą do tej prostej i okręgu, więc muszą spełniać równania je opisujące na raz.
![]()
Zauważ, że z równania prostej masz od razu wyznaczoną zmienną y. Aby uzyskać równanie z jedną zmienną wystarczy, że do równania okręgu za y podstawisz równanie prostej.
![]()
![]()
![]()
![]()
Pamiętaj, że pierwiastkując obustronnie musisz rozważyć przypadek dodatni i ujemny.
![]()
Drugie współrzędne obu tych punktów będą wynosić -3. Więc punkty przecięcia rozważanej prostej i okręgu to:
![]()
![]()
Szukana długość cięciwy to po prostu odległość między tymi dwoma punktami:
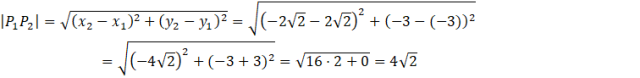

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
