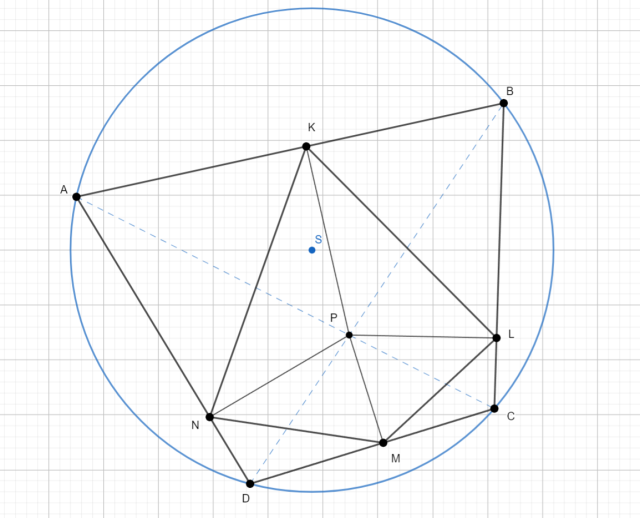
W okrąg jest wpisany czworokąt ABCD. Z punktu P przecięcia przekątnych tego czworokąta poprowadzono wysokości PK, PL, PM, PN odpowiednio w trójkątach ABP, BCP, CDP oraz DAP. Wykaż, że w czworokąt KLMN można wpisać okrąg.
![]()
Czworokąt KANP można wpisać w okrąg.
![]()
Analogicznie
![]()
ale
![]()
![]()
Czyli NP należy do dwusiecznej kąta MNK
Analogicznie MP, LP i KP są dwusiecznymi odpowiednich boków.
Punkt P – przecięcie dwusiecznych
W czworokąt można wpisać okrąg.

Zapisz pary kątów równych jako kąty wpisane oparte na tym samym łuku. Wykazanie równość poszczególnych kątów prowadzi do wniosku, że wysokości leżą na dwusiecznych kątów czworokąta KLMN, a punkt P jest ich przecięciem. Jeżeli dwusieczne kątów czworokąta przecinają się w jednym punkcie, to w ten czworokąt można wpisać okrąg.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
