Policz obwód i pole prostokąta o przekątnych równych 20 cm, z kątem pomiędzy nimi 60°, a następnie wylicz skalę k, w jakiej podobny jest prostokąt o obwodzie lub polu podanym w podpunktach.
Zacznijmy od rysunku:
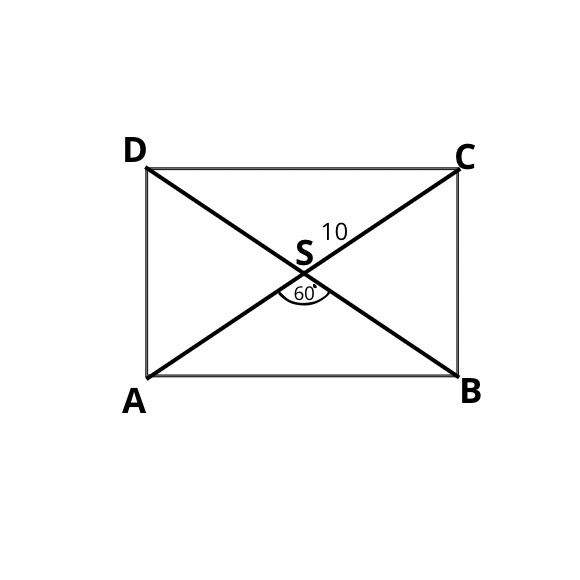
Wiemy, że w prostokącie przekątne przecinają się w połowie, a więc trójkąt ABS jest równoramienny:
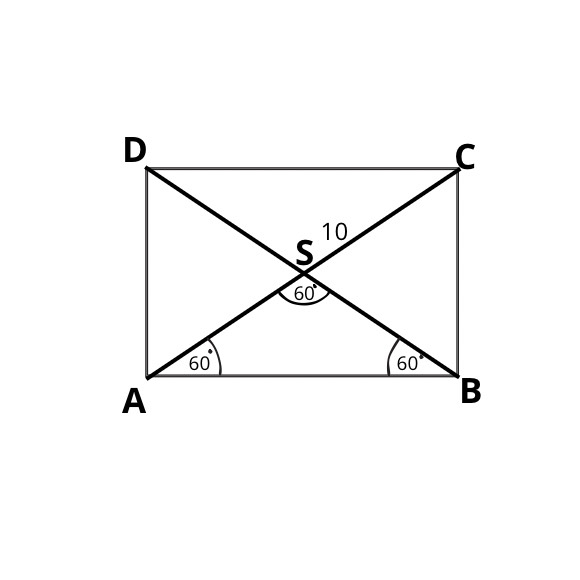
Zauważamy, że trójkąt ABS jest nie tylko równoramienny, ale i równoboczny, więc skoro długość boku AS wynosi 10, to długość boku AB wynosi tyle samo. Korzystając z twierdzenia Pitagorasa liczymy bok BC
![]()
![]()
![]()
![]()
Liczymy teraz pole:
![]()
Sprawdzamy teraz skalę podobieństwa z podanym nam polem:
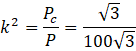


Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
