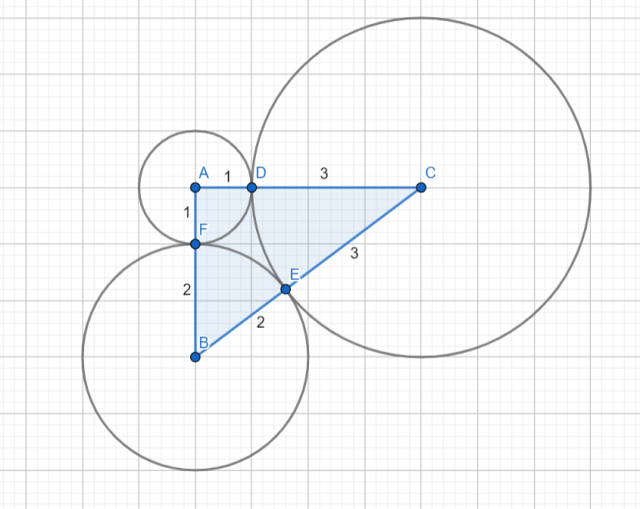
Udowodnij, że trójkąt ABC, którego środki są środkami okręgów stycznych zewnętrznie o promieniach 1, 2 i 3 jest prostokątny.
![]()
![]()
![]()
Twierdzenie odwrotne do twierdzenia Pitagorasa:
![]()
![]()
![]()
Trójkąt jest prostokątny.

Zauważ, że suma każdych dwóch promieni jest równa jednemu bokowi trójkąta. Mając wszystkie 3 długości boków trójkąta, sprawdź, korzystając z twierdzenia odwrotnego do twierdzenia Pitagorasa, czy suma kwadratów dwóch krótszych boków jest równa kwadratowi najdłuższego boku.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
