Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2021

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 15, b) - strona 22

Wyznacz dziedzinę funkcji $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

ODP: Dziedziną funkcji $\text{[math]}$ jest przedział $\text{[math]}$ .

$\text{[math]}$

Zauważ, że długość odcinka $\text{[math]}$ musi być dodatnia, więc $\text{[math]}$ oraz musi być mniejsza od 4, ponieważ obwód, czyli suma długości wszystkich boków trójkąta wynosi 4, więc $\text{[math]}$ .

$\text{[math]}$

Pole musi mieć wartość dodatnią. Oblicz dla jakich $\text{[math]}$ jego wartość jest większa od zera.

Pomnóż całą nierówność przez kwadrat mianownika. Zauważ, że możesz to zrobić, ponieważ kwadrat liczby rzeczywistej jest na pewno dodatni, więc znak nierówności nie zmieni się.

$\text{[math]}$

$\text{[math]}$

Oblicz dla jakich $\text{[math]}$ wartości w każdym z nawiasów (również $\text{[math]}$ ) zerują się.

$\text{[math]}$

$\text{[math]}$

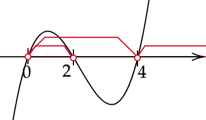
Zaznacz uzyskane rozwiązania na osi. Pamiętaj o uwzględnieniu początkowej nierówności. Ramiona funkcji skieruj do góry, ponieważ współczynnik stojący przy $\text{[math]}$ z największą potęgą jest dodatni. Zaznacz przedziały, w których funkcja jest nad osią.

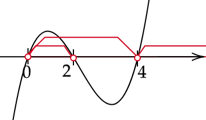
Zapisz wspólny przedział zaznaczonych nierówności.

$\text{[math]}$

Zadanie 4, strona 110, Matematyka wokół nas. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 11., strona 89, Matematyka z plusem. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 38, strona 117, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie 16., strona 203, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie S3., strona 142, Matematyka z Plusem. Klasa 1. Podręcznik. Poziom rozszerzony – rozwiązania i odpowiedzi

Zadanie 5., strona 71, Matematyka z kluczem. Klasa 4. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 8., strona 76, Matematyka. Klasa 2. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 2., strona 52, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie 2., strona 186, MATeMAtyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 3., strona 103, Matematyka z kluczem. Klasa 4. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

2

2

2

2

4

5

6

8

10

12

14

16

18

20

Zadanie 15

22

22

22

22

Pełny spis treści