Udowodnij z odpowiedniej cechy przystawania trójkątów, że w dowolnym równoległoboku przekątne dzielą się na pół.
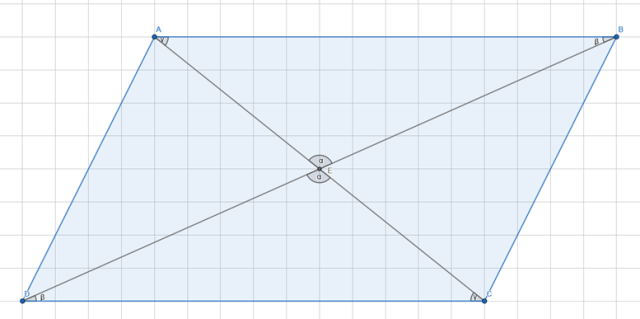
Trójkąty ABE i CDE są przystające (KKK), zatem
![]() , czyli przecięcie przekątnych równoległoboków jest w połowie ich długości. Co należało udowodnić.
, czyli przecięcie przekątnych równoległoboków jest w połowie ich długości. Co należało udowodnić.

Musisz podpisać kąty w jednym trójkącie i następnie korzystając z kątów naprzemianległych i przystających, pozaznaczać je w przeciwnym trójkącie co udowodni ich przystawanie.

Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Zadanie 8.
300Zadanie 5.
305Zadanie 6.
305Zadanie 1.
308Zadanie 2.
309Zadanie 3.
309Zadanie 4.
309Zadanie 1.
308Zadanie 2.
315Zadanie 4.
315Zadanie 5.
315Zadanie 6.
315Zadanie 7.
315Zadanie 8.
315Zadanie 9.
315Zadanie 14.
315Zadanie 2.
319Zadanie 3.
319Zadanie 4.
319Zadanie 5.
319Zadanie 1.
326Zadanie 2.
326Zadanie 5.
326Zadanie 9.
326Zadanie 10.
326Zadanie 11.
326Zadanie 1.
330Zadanie 2.
330Zadanie 9.
331Zadanie 10.
331Zadanie 11.
331Zadanie 12.
331Zadanie 1.
337Zadanie 4.
338Zadanie 5.
338Zadanie 6.
338Zadanie 7.
338Zadanie 8.
338Zadanie 9.
338Zadanie 10.
338Zadanie 11.
338Zadanie 1.
351Zadanie 2.
351Zadanie 3.
351Zadanie 4.
352Zadanie 5.
352Zadanie 6.
352Zadanie 9.
352Zadanie 1.
363Zadanie 2.
363Zadanie 3.
363Zadanie 6.
363Zadanie 10.
365Zadanie 11.
365Zadanie 15.
365
