Udowodnij, że gdy dwie środkowe trójkąta poprowadzone do różnych boków są równe, to ten trójkąt ma równe ramiona.
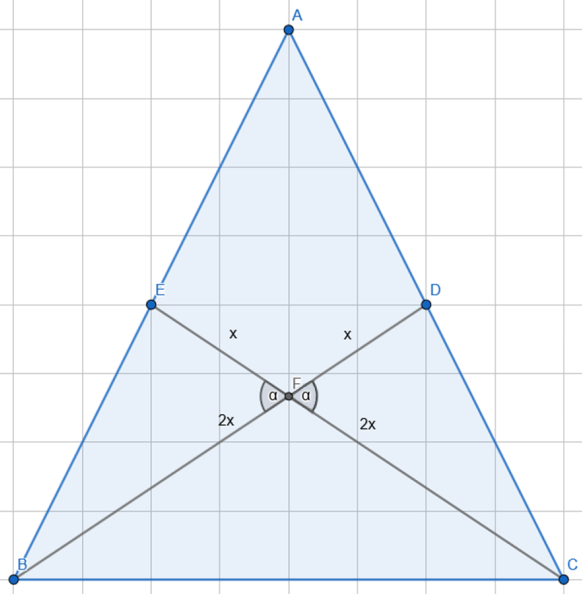
Środkowe przecinając się, dzielą się na dwa odcinki w stosunku 2:1 i korzystając z kątów przystających, trójkąty BEF i CDF są przystające (BKB), zatem
![]() , więc jest to trójkąt równoramienny. Co kończy dowód,
, więc jest to trójkąt równoramienny. Co kończy dowód,

Musisz skorzystać z własności przecinających się środkowych (stosunek 2:1) w trójkącie równoramiennym.

Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Zadanie 8.
300Zadanie 5.
305Zadanie 6.
305Zadanie 1.
308Zadanie 2.
309Zadanie 3.
309Zadanie 4.
309Zadanie 1.
308Zadanie 2.
315Zadanie 4.
315Zadanie 5.
315Zadanie 6.
315Zadanie 7.
315Zadanie 8.
315Zadanie 9.
315Zadanie 14.
315Zadanie 2.
319Zadanie 3.
319Zadanie 4.
319Zadanie 5.
319Zadanie 1.
326Zadanie 2.
326Zadanie 5.
326Zadanie 9.
326Zadanie 10.
326Zadanie 11.
326Zadanie 1.
330Zadanie 2.
330Zadanie 9.
331Zadanie 10.
331Zadanie 11.
331Zadanie 12.
331Zadanie 1.
337Zadanie 4.
338Zadanie 5.
338Zadanie 6.
338Zadanie 7.
338Zadanie 8.
338Zadanie 9.
338Zadanie 10.
338Zadanie 11.
338Zadanie 1.
351Zadanie 2.
351Zadanie 3.
351Zadanie 4.
352Zadanie 5.
352Zadanie 6.
352Zadanie 9.
352Zadanie 1.
363Zadanie 2.
363Zadanie 3.
363Zadanie 6.
363Zadanie 10.
365Zadanie 11.
365Zadanie 15.
365
