Wykonaj rysunek dowolnego kąta ostrego o wierzchołku O. Poprowadzić prostą przecinającą ramiona kąta w punktach A i B tak, by katy przecięcia tej prostej z ramionami kąta miały różne miary. Za pomocą cyrkla i linijki skonstruować we wnętrzu kąta punkt, który jest równoodległy od ramion kąta AOB i jednocześnie równoodległy od punktów A i B
Jest jeden punkt.
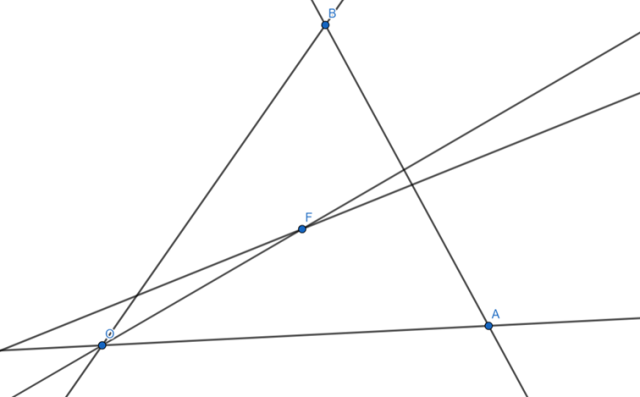

Skonstruuj symetralną odcinka |AB|: wbij cyrkiel w punkt A, ustaw rozwarcie na ponad połowę długości odcinka AB i zaznacz 2 łuki po obu stronach odcinka, później bez zmiany rozwarcia wbij cyrkiel w punkt B i narysuj znowu dwa łuki, punkt ich przecięcia to punkty przez które przechodzi symetralna. Następnie wbij igłę kąt, rozszerz trochę cyrkiel i narysuj łuk łączący ramiona trójkąta AOB, wbij igłę punkt przecięcia łuku i ramion i bez zmieniania ustawienia cyrkla narysuj łuki dalej od kąta i połącz punkt przecięcia się łuków z kątem, ten punkt z wierzchołkiem kąta to dwusieczna kąta.
Przecięcie tych dwóch linii to punkt przecięcia się symetralnej odcinka |AB| i dwusiecznej kąta AOB.

Zadanie 5.
300Zadanie 6.
300Zadanie 7.
300Zadanie 8.
300Zadanie 5.
305Zadanie 6.
305Zadanie 1.
308Zadanie 2.
309Zadanie 3.
309Zadanie 4.
309Zadanie 1.
308Zadanie 2.
315Zadanie 4.
315Zadanie 5.
315Zadanie 6.
315Zadanie 7.
315Zadanie 8.
315Zadanie 9.
315Zadanie 14.
315Zadanie 2.
319Zadanie 3.
319Zadanie 4.
319Zadanie 5.
319Zadanie 1.
326Zadanie 2.
326Zadanie 5.
326Zadanie 9.
326Zadanie 10.
326Zadanie 11.
326Zadanie 1.
330Zadanie 2.
330Zadanie 9.
331Zadanie 10.
331Zadanie 11.
331Zadanie 12.
331Zadanie 1.
337Zadanie 4.
338Zadanie 5.
338Zadanie 6.
338Zadanie 7.
338Zadanie 8.
338Zadanie 9.
338Zadanie 10.
338Zadanie 11.
338Zadanie 1.
351Zadanie 2.
351Zadanie 3.
351Zadanie 4.
352Zadanie 5.
352Zadanie 6.
352Zadanie 9.
352Zadanie 1.
363Zadanie 2.
363Zadanie 3.
363Zadanie 6.
363Zadanie 10.
365Zadanie 11.
365Zadanie 15.
365
