Mając dany zestaw liczb: a, b, c, d, który jednocześnie jest ciągiem arytmetycznym oraz wiedząc, że 2,5 to ich średnia, a 1,25 - wariancja, udowodnij, że
.
T:
Z:
D:
Oblicz sumę podanego zestawu liczb, korzystając ze wzoru na średnią arytmetyczną:
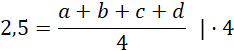
Wykorzystaj definicję ciągu arytmetycznego do uzależnienia liczb b, c, d od a i r:
Uzależnij a od r:
Wykorzystaj wzór na odchylenie standardowe i oblicz r:
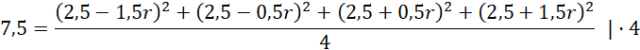
Oblicz a, b, c, d dla r = 1:
Oblicz a, b, c, d dla r = -1:
Zauważ, że podane zestawy liczb składają się z takich samych liczb, dlatego wystarczy, że sprawdzisz czy jeden z nich spełnia tezę:
Co kończy dowód.
Aby poprowadzić ten dowód musisz obliczyć a, b, c, d i pokazać, że spełniają równanie. Wykorzystaj wzór na średnią arytmetyczną
, aby obliczyć ile wynosi suma a + b + c + d. Zauważ, że elementy ciągu różnią się między sobą o r. Wykorzystaj to i uzależnij liczby b, c, d od a i r. Następnie uzależnij a od r, wykorzystując obliczoną sumę. Potem podstaw uzyskane dane do wzoru na wariancję
. Upraszczaj równanie do momentu obliczenia r. Zauważ, że obydwie odpowiedzi r są poprawne, ponieważ nie zmieniają one liczb we zbiorze, tylko ich kolejność. Sprawdź czy spełniają równość podaną w treści.