MATeMAtyka 4. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 5 - strona 176

Ustal, jaką największą objętość, jaką może mieć taki prostopadłościan, jeśli stosunek długości krawędzi podstawy prostopadłościanu jest równy 2, prostopadłościan ten jest wpisany w stożek, którego przekrój osiowy jest trójkątem równobocznym o polu równym $\text{[math]}$ .

$\text{[math]}$ – krawędzie podstawy prostopadłościanu

$\text{[math]}$ – wysokość prostopadłościanu

$\text{[math]}$ – przekątna podstawy prostopadłościanu

$\text{[math]}$ – promień podstawy stożka

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

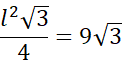
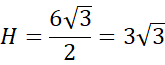
Trójkąty IFC oraz HAC są podobne z cechy KKK, więc trójkąt EFC jest również równoboczny.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

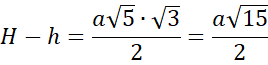
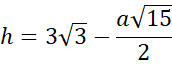
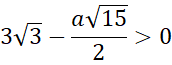
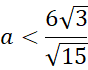
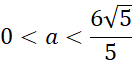
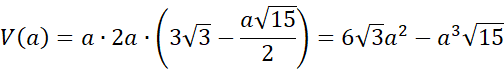
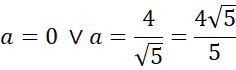
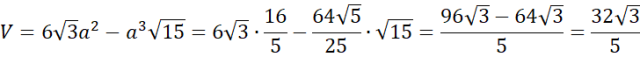
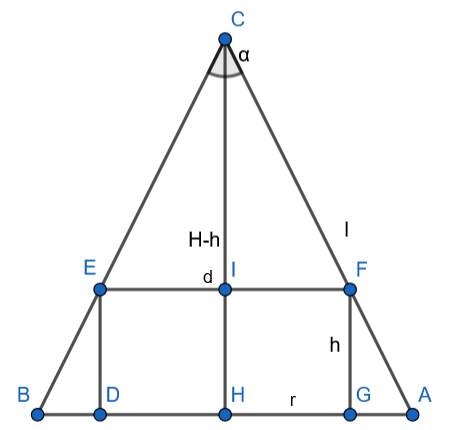
Wyznacz długość tworzącej, promienia i wysokości stożka. Następnie skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć długość przekątnej podstawy prostopadłościanu oraz z podobieństwa trójkątów wyznacz długość wysokości prostopadłościanu.

Następie oblicz objętość bryły – zauważ, że powstanie funkcja zmiennej $\text{[math]}$ , oblicz jej pochodną, miejsce zerowe i największą wartość jaką przyjmuję (miejsce gdzie funkcja rosnąca zmienia się w malejącą). Na koniec dla wyznaczonej długości krawędzi oblicz objętość bryły.

Zadanie 6.42, strona 108, Matematyka 4. Zbiór zadań do liceów i techników. Zakres podstawowy

Zadanie 11, strona 5, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń. Wersja A. Część 1 – rozwiązania i odpowiedzi

Zadanie 13., strona 233, Matematyka. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie 2, strona 50, Matematyka wokół nas. Klasa 6. Zeszyt ćwiczeń. Część 1 – rozwiązania i odpowiedzi

Zadanie 2., strona 60, Matematyka wokół nas. Klasa 4. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 8, strona 23, Matematyka z kluczem. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 13., strona 171, Matematyka. Klasa 1. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 32., strona 51, Matematyka 4. Klasa 4. Zbiór zadań. Zakres rozszerzony - rozwiązania i odpowiedzi

Zadanie 5., strona 108, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 6, strona 5, Matematyka z plusem. Klasa 5. Zeszyt Ćwiczeń – rozwiązania i odpowiedzi

Ćwiczenie 1

138

138

138

138

138

Ćwiczenie 4

139

139

139

Ćwiczenie 5

139

139

139

Zadanie 1

139

139

139

139

Zadanie 2

139

139

139

139

139

139

139

139

140

Zadanie 8

140

140

140

140

140

140

140

140

Zadanie 14

140

140

140

141

141

141

142

Ćwiczenie 5

142

142

142

Ćwiczenie 6

142

142

142

Ćwiczenie 7

143

143

143

Zadanie 1

143

143

143

143

143

Zadanie 2

143

143

143

Zadanie 3

143

143

143

Zadanie 4

143

143

143

143

143

Zadanie 7

144

144

144

144

144

Zadanie 9

144

144

144

144

Zadanie 11

144

144

144

144

Zadanie 13

144

144

144

Zadanie 1

145

145

145

Zadanie 2

145

145

145

Ćwiczenie 1

146

146

146

Ćwiczenie 2

147

147

147

Ćwiczenie 3

147

147

147

147

147

147

Zadanie 1

148

148

148

148

148

Zadanie 3

148

148

148

Zadanie 4

148

148

148

Zadanie 5

148

148

148

148

Zadanie 7

149

149

149

149

Zadanie 9

149

149

149

Zadanie 10

149

149

149

149

149

150

Ćwiczenie 1

151

151

151

151

152

152

Zadanie 1

152

152

152

Zadanie 2

152

152

152

Zadanie 3

153

153

153

153

153

Zadanie 4

153

153

153

153

153

Zadanie 6

153

153

153

153

153

154

Ćwiczenie 1

156

156

156

Ćwiczenie 2

157

157

157

157

Zadanie 1

157

157

157

157

Zadanie 3

157

157

157

157

158

158

158

158

158

158

158

Zadanie 12

158

158

158

158

158

158

Ćwiczenie 1

160

160

160

160

161

161

Zadanie 1

162

162

162

162

Zadanie 3

162

162

162

Zadanie 4

162

162

162

Zadanie 5

162

162

162

Zadanie 6

162

162

162

162

162

162

Ćwiczenie 1

164

164

164

Ćwiczenie 2

164

164

164

Ćwiczenie 3

164

164

164

164

164

165

165

Zadanie 3

165

165

165

165

165

165

165

165

165

165

166

166

166

167

167

167

168

168

168

168

168

168

168

168

168

Zadanie 1

169

169

169

169

Zadanie 2

169

169

169

169

Zadanie 3

170

170

170

170

Zadanie 4

170

170

170

170

170

171

171

171

171

171

171

Zadanie 7

171

171

171

171

171

171

172

172

172

172

172

172

172

172

Zadanie 9

172

172

172

172

172

172

174

174

174

174

174

174

174

174

174

175

175

175

175

175

175

175

175

175

176

176

176

176

176

176

176

176

176

Pełny spis treści