![]()
![]()
![]()
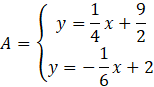
![]()
![]()
![]()
![]()
![]()
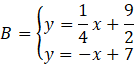
![]()
![]()
![]()
![]()
![]()
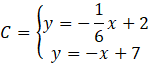
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
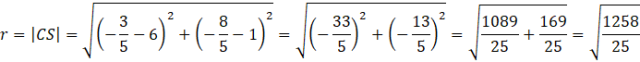
![]()
ODP: Równanie szukanego okręgu ma postać
![]() .
.

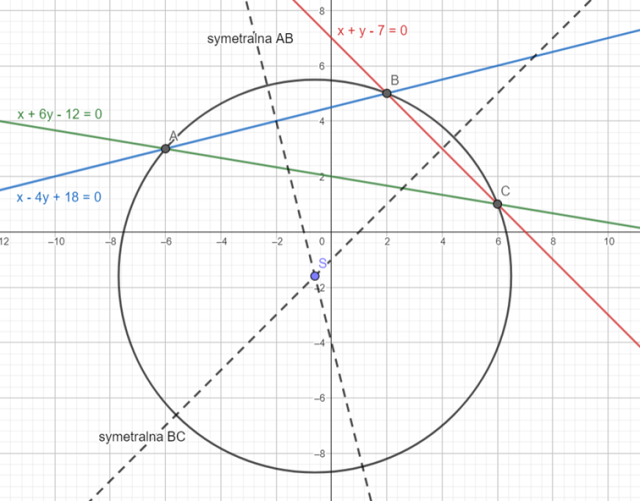
Wykonaj rysunek pomocniczy:
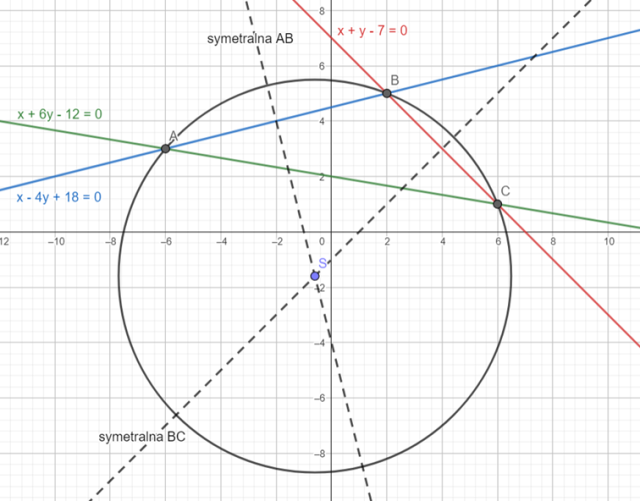
Zapisz wzory prostych podanych w treści zadania w postaci kierunkowej.
![]()
![]()
![]()
Oblicz współrzędne punktu A, czyli miejsce przecięcia prostych AB i AC.
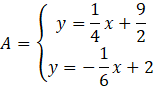
Przyrównaj do siebie wartości
![]() w obu wzorach.
w obu wzorach.
![]()
Z powstałego równania wyznacz wartość
![]()
![]()
![]()
![]()
Zapisz współrzędne punktu A.
![]()
Oblicz współrzędne punktu B, czyli miejsce przecięcia prostych AB i BC.
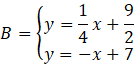
Przyrównaj do siebie wartości
![]() w obu wzorach.
w obu wzorach.
![]()
Z powstałego równania wyznacz wartość
![]()
![]()
![]()
![]()
Zapisz współrzędne punktu B.
![]()
Oblicz współrzędne punktu C, czyli miejsce przecięcia prostych AC i BC.
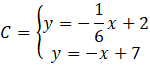
Przyrównaj do siebie wartości
![]() w obu wzorach.
w obu wzorach.
![]()
Z powstałego równania wyznacz wartość
![]()
![]()
![]()
![]()
Zapisz współrzędne punktu C.
![]()
Oblicz środek odcinka AB.
![]()
Zapisz wzór na symetralną odcinka AB, czyli prostą prostopadłą przechodzącą przez jego środek.
![]()
Współczynnik kierunkowy prostych prostopadłych jest przeciwny i odwrotny, na tej podstawie oblicz współczynnik kierunkowy szukanej prostej.
![]()
![]()
Pod wzór szukanej prostej podstaw wyznaczoną wartość
![]() oraz współrzędne środka odcinka AB, aby obliczyć wartość współczynnika
oraz współrzędne środka odcinka AB, aby obliczyć wartość współczynnika
![]()
![]()
![]()
Zapisz wzór szukanej prostej
![]()
Podobnie postąp ze znalezieniem wzoru na symetralną odcinka BC. Na początku oblicz jego środek.
![]()
Zapisz wzór na symetralną odcinka BC, czyli prostą prostopadłą przechodzącą przez jego środek.
![]()
Współczynnik kierunkowy prostych prostopadłych jest przeciwny i odwrotny, na tej podstawie oblicz współczynnik kierunkowy szukanej prostej.
![]()
![]()
Pod wzór szukanej prostej podstaw wyznaczoną wartość
![]() oraz współrzędne środka odcinka BC, aby obliczyć wartość współczynnika
oraz współrzędne środka odcinka BC, aby obliczyć wartość współczynnika
![]()
![]()
![]()
Zapisz wzór szukanej prostej
![]()
Zauważ, że obliczone powyżej symetralne przetną się w środku okręgu. Porównaj więc ich wartości
![]() , aby obliczyć współrzędne środka.
, aby obliczyć współrzędne środka.
![]()
![]()
![]()
![]()
![]()
![]()
Zauważ, że promień okręgu jest równy odległości środka S od jednego z punktów A, B, C. Na tej podstawie oblicz długość odcinka |AS|, |BS| lub |CS|.
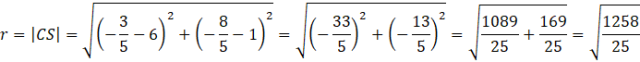
Na koniec zapisz równanie szukanego okręgu.
![]()