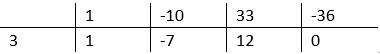
Wyznacz rozwiązania nierówności , której lewa strona jest szeregiem geometrycznym zbieżnym.

Zapisz iloraz ciągu. Zauważ, że każdy kolejny wyraz zwiększa się razy.

Wyznacz dziedzinę, czyli wyklucz , dla których mianownik powyższego ułamka zeruję się.

Zauważ, że aby istniała suma nieskończonego ciągu geometrycznego, to musi być spełniony warunek:

Skorzystaj z tego, że wartość bezwzględną z ilorazu możesz zamienić na iloraz wartości bezwzględnych.

Skorzystaj z tego, że nierówność typu możesz zapisać jako

Zapisz przedział, który musi spełniać lewa strona nierówności zawartej w treści zadania.

Skorzystaj ze wzoru na sumę wyrazów nieskończonego ciągu geometrycznego.

Pod powyższe równanie podstaw znane wartości i wyznacz z niego wartość

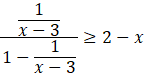
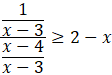
Pomnóż całą nierówność przez kwadrat mianownika ułamka znajdującego się z lewej strony nierówności. Zauważ, że możesz to zrobić, ponieważ kwadrat jakiejkolwiek liczby jest zawsze dodatni, więc znak nierówności nie zmieni się.

Skorzystaj ze wzoru skróconego mnożenia na kwadrat różnicy: , wymnóż nawiasy i przenieś wszystkie wartości na lewą stronę nierówności.

Skorzystaj ze schematu Hornera. Narysuj tabelę. W pierwszym wierszu wpisz wszystkie kolejne współczynniki uporządkowanego równania. W lewym dolnym rogu najniższego wiersza tabelki wpisz liczbę, która jest jego jednym z rozwiązań, czyli 3. Przepisz pierwszy współczynnik bez zmian do dolnego wiersza. Tak otrzymaną liczbę 1 pomnóż przez liczbę 3, następnie dodaj liczbę -10. Wynik będący liczbą -7 wpisz do kolejnej komórki dolnego wiersza w schemacie Hornera. Podobnie postępuj z kolejnymi współczynnikami wielomianu.

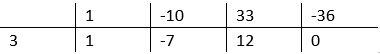
Liczby powstałe w dolnym wierszu są współczynnikami trójmianu. Zapisz powyższe równanie za pomocą iloczynu dwóch nawiasów.

Oblicz pozostałe rozwiązania równania. Zauważ, że powyższe równanie jest równe zero, gdy któryś z nawiasów zeruję się. Rozwiązanie pierwszego nawiasu już znasz. Oblicz deltę i miejsca zerowe drugiego nawiasu, aby wyznaczyć jego rozwiązania.

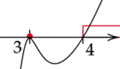
Zaznacz obliczone rozwiązania na osi i przedziały, gdy wykres jest nad lub na osi. Wykres zacznij rysować od góry, ponieważ współczynnik stojący przy z największą potęgą jest dodatni.

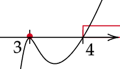
Zapisz wszystkie obliczone powyżej przedziały. Rozwiązaniem będzie ich część wspólna.