Punkt O to punkt przecięcia się przekątnych równoległoboku ABCD, a M leży na AB w taki sposób, że OM jest równoległy do AD. Dodatkowo wiadomo, że |AM| = 8 cm, |AC| = 26 cm oraz |OM| = 7 cm. Należy obliczyć pole równoległobok ABCD.
![]()
![]()
![]()
![]()
Z tw. cosinusów:
![]()
![]()
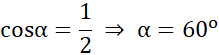
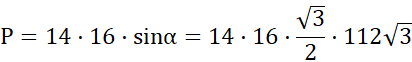

Punkt przecięcia przekątnych w rombie dzieli każdą z nich na połowy. Niech a, b to boki równoległoboku, zaś p i q to jego przekątne. Wówczas zachodzi: ![]()
![]()
![]()

Zadanie 5.2.
127Zadanie 5.8.
127Zadanie 5.11.
128Zadanie 5.12.
128Zadanie 5.18.
129Zadanie 5.23.
129Zadanie 5.24.
129Zadanie 5.25.
129Zadanie 5.26.
130Zadanie 5.27.
130Zadanie 5.30.
130Zadanie 5.34.
130Zadanie 5.35.
130Zadanie 5.39.
131Zadanie 5.40.
131Zadanie 5.51.
132Zadanie 5.52.
132Zadanie 5.53.
132Zadanie 5.54.
132Zadanie 5.55.
132Zadanie 5.56.
133Zadanie 5.58.
133Zadanie 5.59.
133Zadanie 5.61.
133Zadanie 5.63.
134Zadanie 5.68.
134Zadanie 5.70.
134Zadanie 5.78.
136Zadanie 5.79.
136Zadanie 5.80.
136Zadanie 5.81.
136Zadanie 5.82.
137Zadanie 5.86.
137Zadanie 5.87.
137Zadanie 5.12.
139Zadanie 5.14.
140Zadanie 5.16.
140Zadanie 5.26.
141Zadanie 5.27.
141Zadanie 5.29.
141
