Wiadomo, że bok kwadratu ABCD jest równy a. Na każdym z boków tego kwadratu został odłożony odcinek o długości x (jak na rysunku). Musisz udowodnić, że pole pokolorowanego obszaru jest najmniejsze, gdy 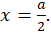
![]()
![]()
![]()

Zamalowana figura jest kwadratem, ponieważ na postawie cechy bkb trójkąty, które powstały są przystające. Skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć pole figury. Ramiona funkcji są skierowane w górę, czyli wartość najmniejsza tej funkcji będzie przyjmowana w wierzchołku. Oblicz pierwszą współrzędną wierzchołka i zauważ, że ma ona wartość ![]()

Zadanie 1.5.
11Zadanie 1.6.
11Zadanie 1.7.
11Zadanie 1.8.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.6.
18Zadanie 2.7.
18Zadanie 2.8.
19Zadanie 2.14.
19Zadanie 3.5.
27Zadanie 3.6.
27Zadanie 3.7.
27Zadanie 3.8.
27Zadanie 3.9.
27Zadanie 3.10.
27Zadanie 3.11.
28Zadanie 3.12.
28Zadanie 3.13.
28Zadanie 3.14.
28Zadanie 3.15.
28Zadanie 3.17.
28Zadanie 3.18.
29Zadanie 3.19.
29Zadanie 3.20.
29Zadanie 3.21.
29Zadanie 4.5.
34Zadanie 4.6.
34Zadanie 4.7.
34Zadanie 4.8.
34Zadanie 4.9.
34Zadanie 4.11.
34Zadanie 4.18.
35Zadanie 4.19.
35Zadanie 4.21.
36Zadanie 5.
36Zadanie 5.5.
40Zadanie 5.6.
40Zadanie 5.7.
40Zadanie 5.8.
40Zadanie 5.10.
40Zadanie 5.14.
41Zadanie 5.15.
41Zadanie 5.16.
41Zadanie 5.17.
41Zadanie 6.5.
46Zadanie 6.6.
47Zadanie 6.7.
47Zadanie 6.8.
47Zadanie 6.9.
47Zadanie 6.11.
48Zadanie 6.12.
48Zadanie 7.5.
54Zadanie 7.8.
54Zadanie 7.9.
54Zadanie 7.10.
54Zadanie 7.14.
55Zadanie 8.7.
60Zadanie 9.1.
71Zadanie 9.2.
71Zadanie 9.3.
71Zadanie 9.4.
72Zadanie 9.5.
72Zadanie 9.14.
73Zadanie 9.15.
73Zadanie 9.16.
73Zadanie 9.24.
74Zadanie 9.25.
74Zadanie 9.26.
74Zadanie 34.
81Zadanie 35.
81Zadanie 36.
81Zadanie 37.
81Zadanie 38.
81Zadanie 40.
81Zadanie 41.
82Zadanie 42.
82Zadanie 44.
82Zadanie 54.
83Zadanie 55.
83Zadanie 58.
83Zadanie 60.
84Zadanie 61.
84Zadanie 63.
84Zadanie 65.
84Zadanie 66.
85Zadanie 67.
85Zadanie 68.
85Zadanie 72.
85Zadanie 73.
85Zadanie 75.
85Zadanie 76.
86Zadanie 86.
86
