Wykaż, że nierówność $\text{[math]}$ spełnia tylko jedna liczba.

$\text{[math]}$

$\text{[math]}$ – 1 miejscem zerowym nierówności

$\text{[math]}$

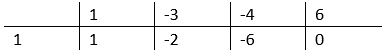
To kończy dowód.

$\text{[math]}$

Wyznacz dziedzinę nierówności. Zauważ, że $\text{[math]}$ musi być liczbą naturalną.

$\text{[math]}$

Skorzystaj ze wzoru na dwumian Newtona: $\text{[math]}$ i zapisz lewą stronę nierówności w najprostszej postaci.

$\text{[math]}$

Powyższe równanie podstaw pod początkową nierówność i przedstaw ją w najprostszej postaci.

$\text{[math]}$

W miejsce $\text{[math]}$ podstaw 1, aby sprawdzić, czy jest ona miejscem zerowym nierówności.

$\text{[math]}$

Skorzystaj ze schematu Hornera, aby obliczyć miejsca zerowe powyższej nierówności.

Narysuj tabelę. W pierwszym wierszu wpisz wszystkie kolejne współczynniki uporządkowanego wielomianu. W lewym dolnym rogu najniższego wiersza tabelki wpisz liczbę, która jest miejscem zerowym dwumianu, czyli 1. Przepisz pierwszy współczynniku bez zmian do dolnego wiersza. Tak otrzymaną liczbę 1 pomnóż przez liczbę 1, która jest miejscem zerowym dwumianu, następnie dodaj liczbę -3. Wynik będący liczbą -2 wpisz do kolejnej komórki dolnego wiersza w schemacie Hornera. Podobnie postępuj z kolejnymi współczynnikami wielomianu.

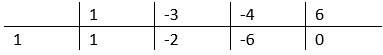
Liczby powstałe w dolnym wierszu są współczynnikami trójmianu, który powstał po dzieleniu. Zapisz go.

$\text{[math]}$

Oblicz rozwiązania drugiego nawiasu, czyli deltę i miejsca zerowe.

$\text{[math]}$

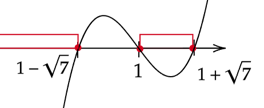
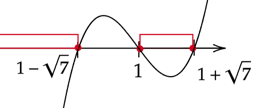
Rozwiązania nierówności zaznacz na osi. Wykres zacznij rysować od góry, ponieważ współczynnik stojący przy $\text{[math]}$ z najwyższą potęgą jest dodatni. Zaznacz przedziały gdy wykres jest pod lub na osi.