Wyznacz równanie okręgu stycznego do prostych
i
przechodzącego przez punkt
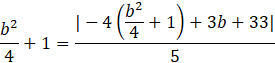
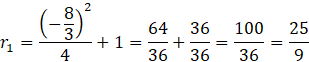
ODP: Szukany okrąg ma równanie
lub
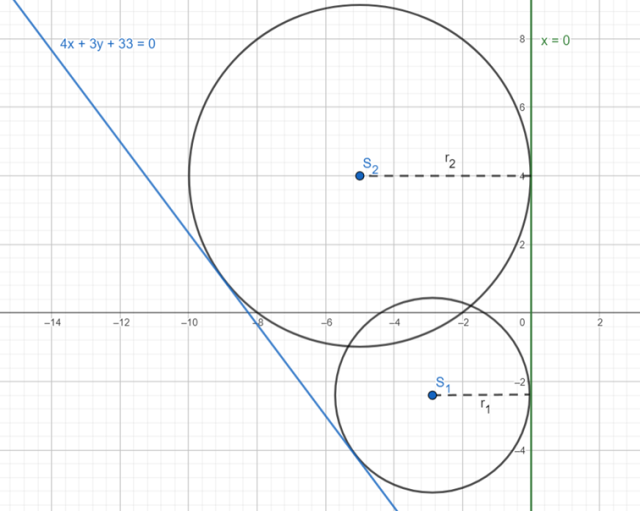
Wykonaj rysunek pomocniczy:
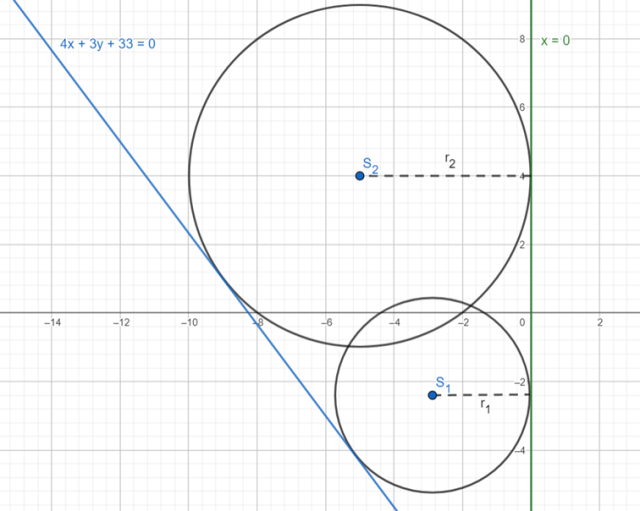
Zapisz środek okręgu jako:
Skorzystaj ze wzoru na odległość punktu od prostej i oblicz odległość środka okręgu od prostej
. Zauważ, że taka odległość będzie równa długości promienia.
Z rysunku możesz odczytać, że
Pod wzór na równanie okręgu podstaw wyznaczoną wartość
oraz współrzędne punktu
Zauważ wzór skróconego mnożenia na kwadrat różnicy i z powyższego równania wyznacz wartość
Ponownie skorzystaj ze wzoru na odległość punktu od prostej, czyli środka okręgu od prostej
Zauważ, że będzie to długość promienia.
Pod powyższe równanie podstaw wyznaczoną wartość
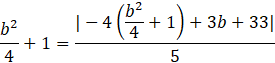
Powyższe równanie przedstaw w najprostszej postaci.
Skorzystaj z tego, że równanie typu:
możesz zapisać w postaci
.
Doprowadź powyższe równania do najprostszych postaci.
Oblicz rozwiązania każdego z powyższych równań, czyli ich deltę i miejsca zerowe
Zauważ, że aby równanie miało rozwiązania to delta musi być większa od zera. Bierzesz więc pod uwagę tylko pierwsze z równań.
Dla każdej z wyliczonych wartości
oblicz długość promienia i wartość pierwszej współrzędnej środka okręgu
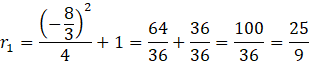
Pod wzór na równanie okręgu podstaw obliczone powyżej wartości i zapisz ich wzory.
