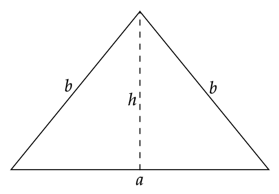
![]() – podstawa trójkąta
– podstawa trójkąta
![]() – ramię trójkąta
– ramię trójkąta
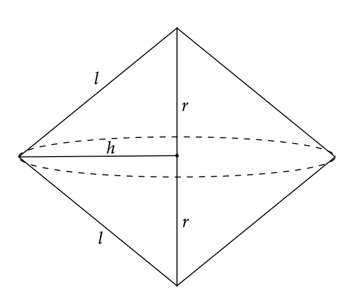
![]() – promień podstawy każdego ze stożków
– promień podstawy każdego ze stożków
![]() – tworząca każdego ze stożków
– tworząca każdego ze stożków
![]() - wysokość każdego ze stożków
- wysokość każdego ze stożków
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP: Szukane długości boków trójkąta to
![]()

Oznacz jako:
![]() – podstawa trójkąta
– podstawa trójkąta
![]() – ramię trójkąta
– ramię trójkąta
Wykonaj rysunki pomocnicze:
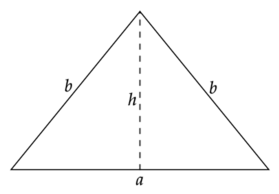
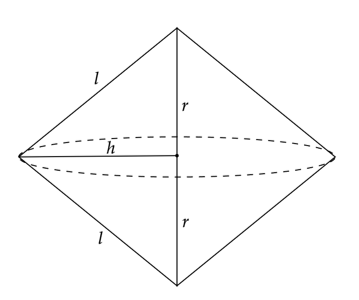
Na podstawie rysunków zauważ, że:
![]() – promień podstawy każdego ze stożków
– promień podstawy każdego ze stożków
![]() – tworząca każdego ze stożków
– tworząca każdego ze stożków
![]() - wysokość każdego ze stożków
- wysokość każdego ze stożków
Zapisz obwód trójkąta za pomocą zmiennych
![]() i
i
![]() oraz
oraz
![]() i
i
![]()
![]()
![]()
Z powyższego równania wyznacz wartość tworzącej stożka, czyli
![]()
![]()
Zauważ, że aby trójkąt istniał, to promień musi mieć długość mniejszą niż tworząca oraz jego długość musi być większa od zera.
![]()
Na tej podstawie wyznacz dziedzinę, do której należy
![]()
![]()
![]()
![]()
Zauważ, że trójkąt zawierający promień, wysokość i tworzącą stożka jest prostokątny. Skorzystaj z twierdzenia Pitagorasa aby obliczyć długość wysokości.
![]()
Pod powyższe równanie podstaw wyznaczoną wartość
![]()
![]()
Zauważ wzór skróconego mnożenia na kwadrat różnicy i z powyższego równania wyznacz wartość
![]()
![]()
![]()
Zapisz wzór na objętość bryły przedstawionej na rysunku, czyli dwóch stożków, każdy o promieniu
![]() i wysokości
i wysokości
![]()
![]()
Pod wzór na objętość podstaw wyznaczoną wartość
![]() . Zauważ, że powstała funkcja zmiennej
. Zauważ, że powstała funkcja zmiennej
![]() Przedstaw jej wzór w najprostszej postaci.
Przedstaw jej wzór w najprostszej postaci.
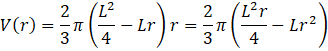
Oblicz pochodną funkcji
![]()
![]()
Wyznacz miejsca zerowe powstałej pochodnej, czyli przyrównaj jej wartość do zera.
![]()
Z powstałego równania wyznacz wartość
![]()
![]()
![]()
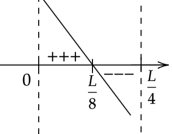
Zaznacz obliczone rozwiązanie na osi. Wykres zacznij rysować od dołu, ponieważ współczynnik stojący przy
![]() z największą potęgą jest ujemny. Pamiętaj o uwzględnieniu dziedziny.
z największą potęgą jest ujemny. Pamiętaj o uwzględnieniu dziedziny.
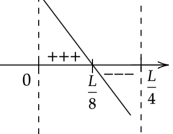
Oznacza to, że pochodna w przedziale
![]() ma jedno miejsce zerowe
ma jedno miejsce zerowe
![]() i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja
![]() rośnie w przedziale
rośnie w przedziale
![]() ,a maleje w przedziale
,a maleje w przedziale
![]() . Więc będzie to największa wartość pochodnej.
. Więc będzie to największa wartość pochodnej.
![]()
Oblicz długości boków
![]() i
i
![]() trójkąta, dla których powstała bryła ma największą objętość.
trójkąta, dla których powstała bryła ma największą objętość.
![]()
![]()