W tym zadaniu musisz znaleźć niewiadoma liczbę k tak, żeby zestaw liczb spełniał opisane warunki, a następnie dla otrzymanego zestawu obliczyć wariancje i odchylenie standardowe.
Dany jest zestaw liczb naturalnych: 2, 3, 3, 3, 3, 5, 5, 5, 6, k. Ich średnia wynosi:
![]()
Mogą zachodzić trzy przypadki, gdy mediana wynosi: 4, 3 lub ![]()
Przypadek 1:
![]()
![]()
![]()
Warunki zadania są spełnione.
Przypadek 2:
![]()
![]()
![]()
Sprzeczność:
Przypadek 3:
![]()
![]()
![]()
![]()
Warunki zadania są spełnione.
Ostatecznie k = 5.
Mamy zestaw liczb: : 2, 3, 3, 3, 3, 5, 5, 5, 5, 6.
![]()
2 – 4 = -2
3 – 4 = -1
5 – 4 = 1
6 – 4 = 2
![]()
![]()
-Liczba k wynosi 5. Wtedy wariancja i odchylenie standardowe tego zestawu liczb wynoszą odpowiednio 1,6 oraz 1,26.

Dla zbioru danych ![]()
![]()
Wariancje obliczysz ze wzoru:
![]()
Odchylenie standardowe wyznaczysz ze wzoru:
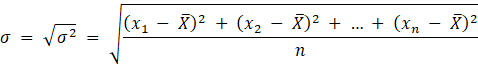

Zadanie 1
276Zadanie 4
276Zadanie 8
277Zadanie 17
278Zadanie 20
278Zadanie 2
279Zadanie 6
280Zadanie 7
280Zadanie 8
280Zadanie 9
280Zadanie 10
281Zadanie 11
281Zadanie 12
281Zadanie 13
282Zadanie 18
283Zadanie 20
283Zadanie 23
283Zadanie 1
284Zadanie 3
284Zadanie 4
284Zadanie 7
285Zadanie 14
286Zadanie 15
286Zadanie 22
287Zadanie 1
288Zadanie 8
289Zadanie 16
291Zadanie 1
292Zadanie 6
292Zadanie 8
293
