W tym zadaniu musisz określić, czy istnieje taki zestaw liczb całkowitych spełniający opisane warunki.
Skoro odchylenie standardowe wynosi ![]()
Niech a, b, c, d, e będą liczbami całkowitymi z tego zestawu. Powinna wtedy zachodzić równość:
![]()
![]()
Wyrażenie po lewej stronie jest liczba całkowita, a po prawej nie, zatem nie istnieje taki zestaw liczb.

Dla zbioru danych ![]()
![]()
Wariancje obliczysz ze wzoru:
![]()
Można ja również określić jako:
![]()
Odchylenie standardowe wyznaczysz ze wzoru:
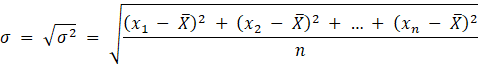

Zadanie 1
276Zadanie 4
276Zadanie 8
277Zadanie 17
278Zadanie 20
278Zadanie 2
279Zadanie 6
280Zadanie 7
280Zadanie 8
280Zadanie 9
280Zadanie 10
281Zadanie 11
281Zadanie 12
281Zadanie 13
282Zadanie 18
283Zadanie 20
283Zadanie 23
283Zadanie 1
284Zadanie 3
284Zadanie 4
284Zadanie 7
285Zadanie 14
286Zadanie 15
286Zadanie 22
287Zadanie 1
288Zadanie 8
289Zadanie 16
291Zadanie 1
292Zadanie 6
292Zadanie 8
293
