W tym zadaniu musisz znaleźć średnia i odchylenie standardowe podanego zestawu liczb, a następnie obliczyć odchylenie standardowe danych zmienionych zgodnie z warunkami zadania i porównać otrzymane wyniki.
Dla kwot 1, 2, 3, 4, 5, 6, 7:
![]()
1 – 4 = -3
2 – 4 = -2
3 – 4 = -1
4 – 4 = 0
5 – 4 = 1
6 – 4 = 2
7 – 4 = 3
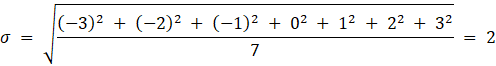
Średnia kwota wrzucana przez Anie do skarbonki to 4 złote. Odchylenie standardowe w tym przypadku wynosi 2 złote.
Dla kwot dwa razy większych, czyli 2, 4, 6, 8, 10, 12, 14:
![]()
2 – 8 = -6
4 – 8 = -4
6 – 8 = -2
8 – 8 = 0
10 – 8 = 2
12 – 8 = 4
14 – 8 = 6
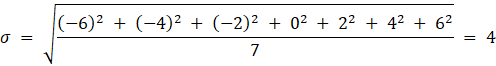
Gdyby Ania zwiększyła kwoty dwukrotnie, to odchylenie standardowe wynosiło by 4, czyli wzrosło by dwukrotnie.
Dla kwot trzy razy większych, czyli 3, 6, 9, 12, 15, 18, 21:
![]()
3 – 12 = -9
6 – 12 = -6
9 – 12 = -3
12 – 12 = 0
15 – 12 = 3
18 – 12 = 6
21 – 12 = 9
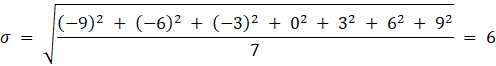
Gdyby Ania zwiększyła kwoty trzykrotnie, to odchylenie standardowe wynosiło by 6, czyli wzrosło by trzykrotnie.

Dla zbioru danych ![]()
![]()
Wariancje obliczysz ze wzoru:
![]()
Odchylenie standardowe wyznaczysz ze wzoru:
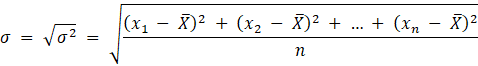

Zadanie 1
276Zadanie 4
276Zadanie 8
277Zadanie 17
278Zadanie 20
278Zadanie 2
279Zadanie 6
280Zadanie 7
280Zadanie 8
280Zadanie 9
280Zadanie 10
281Zadanie 11
281Zadanie 12
281Zadanie 13
282Zadanie 18
283Zadanie 20
283Zadanie 23
283Zadanie 1
284Zadanie 3
284Zadanie 4
284Zadanie 7
285Zadanie 14
286Zadanie 15
286Zadanie 22
287Zadanie 1
288Zadanie 8
289Zadanie 16
291Zadanie 1
292Zadanie 6
292Zadanie 8
293
