Oblicz podane pierwiastki i sprawdź, które zdania są prawdziwe:
A. $\text{[math]}$ jest liczbą wymierną.
B. $\text{[math]}$ jest liczbą całkowitą.
C. $\text{[math]}$ jest liczbą mniejszą od 15.
D. $\text{[math]}$ jest liczbą większą od 0,05.

$\text{[math]}$

$\text{[math]}$ – jest liczbą wymierną

$\text{[math]}$

$\text{[math]}$ - nie jest liczbą całkowitą

$\text{[math]}$

$\text{[math]}$ – jest większe od 15

$\text{[math]}$

$\text{[math]}$ – jest większe od $\text{[math]}$

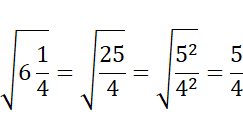
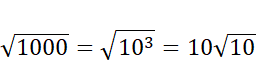
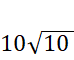
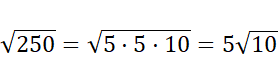
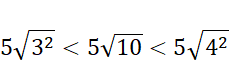
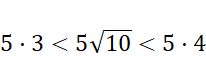
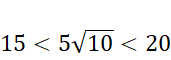
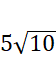
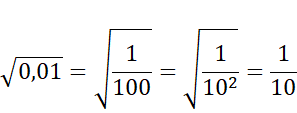
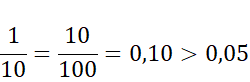
Odpowiedź: A,D

Najpierw zamień liczbę pod pierwiastkiem na ułamek niewłaściwy, później wiedząc, że pierwiastek ilorazu jest ilorazem pierwiastków oblicz oba pierwiastki (znajdź liczbę, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem). Następnie pamiętając, że liczby wymierne to liczby, które można zapisać w postaci ilorazu dwóch liczb całkowitych, stwierdź, że zdanie A jest prawdziwe.

Liczbę 1000, która jest pod pierwiastkiem drugiego stopnia przedstaw jako 3 potęga liczby 10. Wyciągając 10 do potęgi drugiej spod pierwiastka, otrzymasz 10 przed pierwiastkiem razy pierwiastek z 10. Wiesz, że żadna liczba całkowita podniesiona do drugiej potęgi nie daje 10, dlatego wyjściowa liczba nie może być całkowita.

Liczbę 250 zapisz jako iloczyn liczb; 5,5,10 postępuj tak jak w poprzednim podpunkcie, a następnie ogranicz otrzymaną liczbę z dwóch stron przez 5 razy pierwiastek, który potrafisz policzyć. Wylicz te pierwiastki (znajdź liczbę, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem), a następnie zauważysz, że wyjściowa liczba jest większa od 15.

Liczbę pod pierwiastkiem zamień na ułamek prosty, a następnie, wiedzą, że pierwiastek ilorazu jest ilorazem pierwiastków oblicz ten pierwiastek (znajdź liczbę, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem). Potem zamień tę liczbę z powrotem na ułamek dziesiętny i porównaj z podaną liczbą.