a = 6 cm,
b = 6 cm
c = 6 ∙ 50 % = 6 ∙ 0,5 = 3 cm
V = 6 ∙ 6 ∙ 3 = 108 cm3
Pc = 2 ∙Pp + Pb
Pc = 2 ∙ 6 ∙ 6 + 4 ∙ 6 ∙ 3 = 72 + 72 = 144 cm2
a = b = 6 cm, c = 3 cm
a’ = 6 : 3 = 2 cm
c’ = 3 : 3 = 1 cm

Objętość prostopadłościanu wyrażona jest wzorem: V = a ∙ b ∙ c, gdzie a, b, c oznaczają długość, szerokość i wysokość prostopadłościanu.
a = 6 cm, b = 6 cm
Wiadomo, że wysokość stanowi 50% krawędzi podstawy.
c = 6 ∙ 50% = 6 ∙ 0,5 = 3 cm
V = 6 ∙ 6 ∙ 3 = 108 cm3
Teraz oblicz pole całkowite. Pole całkowite jest sumą dwóch pól wielokąta w podstawie i pola bocznego. Pole całkowite opisuje poniższy wzór:
Pc = 2 ∙Pp + Pb
Podstaw dane do wzoru i wykonaj obliczenia.
Pc = 2 ∙ 6 ∙ 6 + 4 ∙ 6 ∙ 3 = 72 + 72 = 144 cm2
Teraz oblicz, jaką długość krawędzi, będą miały boki tego prostopadłościanu w skali 1 : 3. Skala jest to miara pomniejszenia w stosunku do wymiarów rzeczywistych. Określa się ją jako stosunek wymiaru przeskalowanego przedmiotu do odpowiadającego mu wymiaru rzeczywistego. Obie te wielkości wyrażane są w tych samych jednostkach. Skala 1 : 3, oznacza, że 1 cm odpowiada 3 cm w rzeczywistości. Długość krawędzi narysowanego prostopadłościanu będzie zatem wynikiem dzielenia ich długości rzeczywistej wyrażonej w cm przez 3.
Wiadomo, że a = b = 6 cm, c = 3 cm. Zatem:
a’ = 6 : 3 = 2 cm
c’ = 3 : 3 = 1 cm
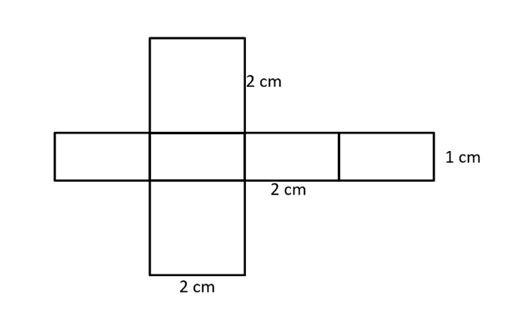
Narysuj siatkę tego prostopadłościanu. Siatkę graniastosłupa prostego można narysować na kilka sposobów. W tym zadaniu musisz narysować siatkę prostopadłościany. Wiadomo, że ściany boczne są prostokątami o znanych wymiarach: 2 cm x 1 cm. Narysuj obok siebie cztery przystające prostokąty. Następnie dorysuj podstawy graniastosłupa, czyli dwa kwadraty o boku 2 cm. Aby złożona siatka utworzyła bryłę podstawy, muszą znaleźć się na dwóch przeciwległych do siebie bokach prostokąta tworzącego ścianę boczną.
