Wyznacz obwód pojedynczej płytki, jeśli z jednakowych prostokątnych płytek ułożono kwadrat o polu równym
![]() .
.
![]() – bok powstałego kwadratu
– bok powstałego kwadratu
![]() – długość pojedynczej płytki
– długość pojedynczej płytki
![]() – szerokość pojedynczej płytki
– szerokość pojedynczej płytki
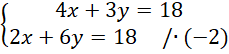
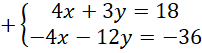
![]()
![]()
![]()
![]()
![]()
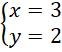
![]()

Skorzystaj z tego, że pole kwadratu o boku
![]() można obliczyć ze wzoru
można obliczyć ze wzoru
![]() i oblicz długość jego boku. Następnie długość i szerokość pojedynczej płytki oznacz jako
i oblicz długość jego boku. Następnie długość i szerokość pojedynczej płytki oznacz jako
![]() i
i
![]() . Własności podane w treści zadania zapisz za pomocą równań. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Zauważ, że całe drugie równanie należy pomnożyć przez (-2), aby współczynniki znajdujące się przy
. Własności podane w treści zadania zapisz za pomocą równań. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Zauważ, że całe drugie równanie należy pomnożyć przez (-2), aby współczynniki znajdujące się przy
![]() były przeciwne. Następnie dodaj do siebie stronami oba równania znajdujące się w układzie. Z powstałego równania wyznacz wartość
były przeciwne. Następnie dodaj do siebie stronami oba równania znajdujące się w układzie. Z powstałego równania wyznacz wartość
![]() . Wyznaczoną wartość
. Wyznaczoną wartość
![]() podstaw pod jedno z początkowych równań i wyznacz z niego wartość
podstaw pod jedno z początkowych równań i wyznacz z niego wartość
![]() Na koniec oblicz obwód pojedynczej płytki.
Na koniec oblicz obwód pojedynczej płytki.

Zadanie 1
126Zadanie 3
127Zadanie 4
127Zadanie 5
127Zadanie 6
127Zadanie 7
127Ćwiczenie 1
129Ćwiczenie 2
130Ćwiczenie 3
130Ćwiczenie 4
132Zadanie 1
132Zadanie 2
132Zadanie 3
133Zadanie 4
133Zadanie 5
133Zadanie 6
133Zadanie 7
133Zadanie 8
133Ćwiczenie 1
134Ćwiczenie 2
135Ćwiczenie 3
136Ćwiczenie 4
136Ćwiczenie 5
139Zadanie 1
139Zadanie 2
139Zadanie 3
139Zadanie 4
139Zadanie 1
140Zadanie 2
140Zadanie 3
140Ćwiczenie 2
141Ćwiczenie 4
143Zadanie 1
151Zadanie 2
151Zadanie 1
153Zadanie 1
154Zadanie 2
154Zadanie 3
154Zadanie 4
154Zadanie 5
154Zadanie 1
155Zadanie 2
155Zadanie 3
155Zadanie 4
155Zadanie 5
155Zadanie 6
155Zadanie 7
155
