Ustal, czy układ równań
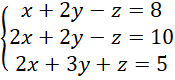 spełnia trójka liczb całkowitych.
spełnia trójka liczb całkowitych.
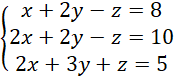
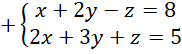
![]()
![]()
![]()
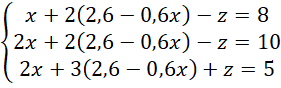
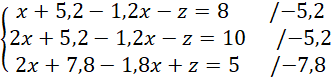
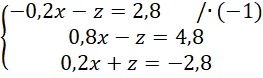
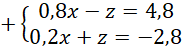
![]()
![]()
![]()
![]()
![]()
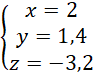
Układu nie spełnia trójka liczb całkowitych.

Zauważ, że współczynniki przy
![]() w pierwszym i trzecim równaniu są przeciwne, dodaj więc je do siebie stronami i z powstałego równania wyznacz wartość
w pierwszym i trzecim równaniu są przeciwne, dodaj więc je do siebie stronami i z powstałego równania wyznacz wartość
![]() .
.
Wyznaczoną wartość
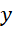 podstaw pod każde z podanych równań, a następnie przedstaw je w najprostszej postaci.
podstaw pod każde z podanych równań, a następnie przedstaw je w najprostszej postaci.
Zauważ, że współczynniki przy
![]() w drugim i trzecim równaniu są przeciwne, dodaj je więc do siebie stronami i wyznacz z niego wartość
w drugim i trzecim równaniu są przeciwne, dodaj je więc do siebie stronami i wyznacz z niego wartość
![]() .
.
Na koniec wyznaczoną wartość
![]() podstaw pod jedno z wcześniejszych równań, wyznacz z niego wartość
podstaw pod jedno z wcześniejszych równań, wyznacz z niego wartość
![]() oraz wartość
oraz wartość
![]() i ustal, czy rozwiązaniem układu równań są liczby całkowite.
i ustal, czy rozwiązaniem układu równań są liczby całkowite.

Zadanie 1
126Zadanie 3
127Zadanie 4
127Zadanie 5
127Zadanie 6
127Zadanie 7
127Ćwiczenie 1
129Ćwiczenie 2
130Ćwiczenie 3
130Ćwiczenie 4
132Zadanie 1
132Zadanie 2
132Zadanie 3
133Zadanie 4
133Zadanie 5
133Zadanie 6
133Zadanie 7
133Zadanie 8
133Ćwiczenie 1
134Ćwiczenie 2
135Ćwiczenie 3
136Ćwiczenie 4
136Ćwiczenie 5
139Zadanie 1
139Zadanie 2
139Zadanie 3
139Zadanie 4
139Zadanie 1
140Zadanie 2
140Zadanie 3
140Ćwiczenie 2
141Ćwiczenie 4
143Zadanie 1
151Zadanie 2
151Zadanie 1
153Zadanie 1
154Zadanie 2
154Zadanie 3
154Zadanie 4
154Zadanie 5
154Zadanie 1
155Zadanie 2
155Zadanie 3
155Zadanie 4
155Zadanie 5
155Zadanie 6
155Zadanie 7
155
