Zadanie
W tym zadaniu oblicz odchylenia standardowe zestawów liczb A i B oraz sformułuj wniosek.
A: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4
B: 11, 12, 12, 13, 13, 13, 14, 14, 14, 14
Rozwiązanie
A:
=
σ =
= 1
B:
=
σ =
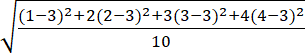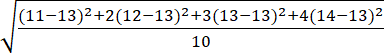= 1
Możemy zauważyć, że w zestawie B zwiększono wartości liczb, dodając do liczb z zestawu A 10. Zatem jeżeli wszystkie liczby z danego zestawu danych zwiększymy o stałą wartość, to odchylenie standardowe nie ulegnie zmianie.
Wyjaśnienie
Odchylenie standardowe jest to pierwiastek z wariancji. Odchyleniem standardowym liczb x1, x2, …, xn nazywamy liczbę σ określoną za pomocą wzoru: σ =
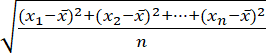. Średnią arytmetyczną n liczb: x1, x2, …, xn nazywamy liczbę:
, gdzie x1, x2, …, xn to kolejne liczby, natomiast n oznacza ilość liczb w danym zestawie danych.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
4. Statystyka
171
4.1. Średnia arytmetyczna
172
Ćwiczenie 5.
173Zadanie 2.
174Zadanie 3.
174Zadanie 4.
174Zadanie 5.
174Zadanie 6.
175Zadanie 8.
175Zadanie 10.
175
4.2. Mediana, skala centylowa i dominanta
176
Ćwiczenie 1.
176Ćwiczenie 2.
176Ćwiczenie 4.
176Ćwiczenie 6.
178Ćwiczenie 7.
178Ćwiczenie 9.
179Zadanie 1.
179Zadanie 3.
180Zadanie 4.
179Zadanie 5.
181Zadanie 7.
181
4.3. Odchylenie standardowe
182
Ćwiczenie 1.
183Zadanie 1.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 8.
185Zadanie 9.
185
Inne miary rozrzutu danych – warto wiedzieć
188
Zadanie 1.
188Zadanie 3.
188
4.4. Średnia ważona
189
Ćwiczenie 1.
189Ćwiczenie 2.
189Ćwiczenie 3.
190Ćwiczenie 4.
190Zadanie 3.
191Zadanie 4.
191Zadanie 5.
191Zadanie 6.
191
4.5. Zagadnienia uzupełniające
192
Zestawy powtórzeniowe. Zestaw I
193
Zadanie 1.
193Zadanie 6.
194
Zestawy powtórzeniowe. Zestaw II
194
Zadanie 2.
194Zadanie 5.
195
Zadania testowe
197
Przed obowiązkową maturą z matematyki
198