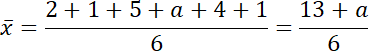
σ2 =
![]()
![]() / ·6
/ ·6
13 + a = 4 – 4
![]() +
+
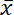 2 + 2 – 4
2 + 2 – 4
![]() + 2
+ 2
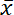 2 + 16 – 8
2 + 16 – 8
![]() +
+
![]() 2 + 25 – 10
2 + 25 – 10
![]() +
+
![]() 2 + a2 – 2a
2 + a2 – 2a
![]() +
+
![]() 2
2
13 + a = 6
![]() 2 –26
2 –26
![]() – 2a
– 2a
![]() + 47 + a2
+ 47 + a2
13 + a = 6
![]() 2 –26
2 –26
![]() – 2a
– 2a
![]() + 47 + a2
+ 47 + a2
13 + a =
![]() + 47 + a2 / · 6
+ 47 + a2 / · 6
78 + 6a = 169 + 26a + a2 – 338 – 26a – 26a – 2a2 + 282 + 6a2
5a2 – 32a + 35 = 0
a1 = 5, a2 = 1,4

Wariancją σ2 liczb: x1, x2, …, xn nazywamy liczbę:
![]() , gdzie
, gdzie
![]() określa średnią arytmetyczną z liczb x1, x2, …, xn. Odchylenie standardowe jest to pierwiastek z wariancji. Odchyleniem standardowym liczb x1, x2, …, xn nazywamy liczbę σ określoną za pomocą wzoru: σ =
określa średnią arytmetyczną z liczb x1, x2, …, xn. Odchylenie standardowe jest to pierwiastek z wariancji. Odchyleniem standardowym liczb x1, x2, …, xn nazywamy liczbę σ określoną za pomocą wzoru: σ =
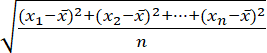 . Średnią arytmetyczną n liczb: x1, x2, …, xn nazywamy liczbę:
. Średnią arytmetyczną n liczb: x1, x2, …, xn nazywamy liczbę:
![]() , gdzie x1, x2, …, xn to kolejne liczby, natomiast n oznacza ilość liczb w danym zestawie danych.
, gdzie x1, x2, …, xn to kolejne liczby, natomiast n oznacza ilość liczb w danym zestawie danych.