W tym zadaniu określ, o ile byłaby wyższa średnia ocen w tej grupie, a o ile w całej klasie, gdyby uczniowie ci na koniec semestru otrzymali ocenę dopuszczającą, a oceny reszty uczniów pozostały bez zmian, jeżeli troje uczniów w grupie I otrzymało na koniec semestru ocenę niedostateczną.
Średnia ocen w grupie I po otrzymaniu ocen dopuszczających przez troje uczniów:
![]() = 3,75
= 3,75
3,75 – 3,5 = 0,25
Średnia w grupie byłaby wyższa o 0,25.
Średnia ocen w całej grupie:
![]() = 3,7
= 3,7
Średnia ocen w klasie po otrzymaniu ocen dopuszczających przez troje uczniów:
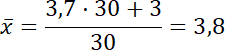
3,8 – 3,7 = 0,1
Średnia w klasie byłaby wyższa o 0,1.

Średnią arytmetyczną n liczb: x1, x2, …, xn nazywamy liczbę:
![]() , gdzie x1, x2, …, xn to kolejne liczby, natomiast n oznacza ilość liczb w danym zestawie danych.
, gdzie x1, x2, …, xn to kolejne liczby, natomiast n oznacza ilość liczb w danym zestawie danych.

Ćwiczenie 5.
173Zadanie 2.
174Zadanie 3.
174Zadanie 4.
174Zadanie 5.
174Zadanie 6.
175Zadanie 8.
175Zadanie 10.
175Ćwiczenie 1.
176Ćwiczenie 2.
176Ćwiczenie 4.
176Ćwiczenie 6.
178Ćwiczenie 7.
178Ćwiczenie 9.
179Zadanie 1.
179Zadanie 3.
180Zadanie 4.
179Zadanie 5.
181Zadanie 7.
181Ćwiczenie 1.
183Zadanie 1.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 8.
185Zadanie 9.
185Zadanie 1.
188Zadanie 3.
188Ćwiczenie 1.
189Ćwiczenie 2.
189Ćwiczenie 3.
190Ćwiczenie 4.
190Zadanie 3.
191Zadanie 4.
191Zadanie 5.
191Zadanie 6.
191Zadanie 1.
193Zadanie 6.
194Zadanie 2.
194Zadanie 5.
195
