(x1 –
) = 167 – 175,2 = –8,2
(x2 –
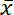) = 169 – 175,2 = –6,2
(x3 –
) = 172 – 175,2 = –3,2
(x4 –
) = 174 – 175,2 = –1,2
(x5 –
) = 175 – 175,2 = –0,2
(x6 –
) = 176 – 175,2 = 0,8
(x7 –
) = 177 – 175,2 = 1,8
(x8 –
) = 178 – 175,2 = 2,8
(x9 –
) = 180 – 175,2 = 4,8
(x10 –
) = 184 – 175,2 = 8,8
(y1 –
) = 69 – 74,0 = –5
(y2 –
) = 67 – 74,0 = –7
(y3 –
) = 74 – 74,0 = 0
(y4 –
) = 70 – 74,0 = –4
(y5 –
) = 70 – 74,0 = –4
(y6 –
) = 74 – 74,0 = 0
(y7 –
) = 78 – 74,0 = 4
(y8 –
) = 76 – 74,0 = 2
(y9 –
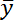) = 82 – 74,0 = 8
(y10 –
) = 80 – 74,0 = 6
r =
r =
r ≈ 0,85
Średnią arytmetyczną n liczb: x1, x2, …, xn nazywamy liczbę:
, gdzie x1, x2, …, xn to wzrost lub masa ciała, w zależności jaką średnią obliczamy, natomiast n oznacza ilość osób. Do zmierzenia korelacji między zmiennymi x i y na podstawie par danych (x1, y1), (x2, y2), …, (xn, yn), których średnie arytmetyczne wynoszą odpowiednio
oblicza się współczynnik korelacji r Pearsona: r =
