Wykaż, że jeśli dwusieczna kąta
przecina przyprostokątną
trójkąta
w punkcie
oraz
, to
.
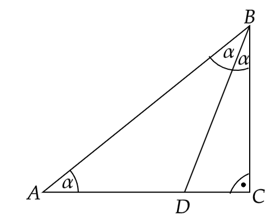
Trójkąt BCD jest trójkątem szczególnym.
To kończy dowód.
Zauważ, że:
– ponieważ trójkąt ADB jest równoramienny
– ponieważ odcinek BD jest dwusieczną kąta ABC
Wprowadź oznaczenia pomocnicze:
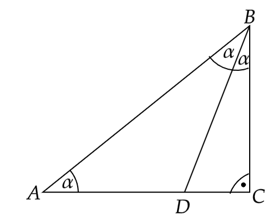
Skorzystaj z tego, że suma miar kątów w trójkącie wynosi
i oblicz miarę kąta
.
Oblicz brakującą miarę kąta CDB w trójkącie BCD. Ponownie skorzystaj z tego, że suma miar kątów w trójkącie wynosi
Zauważ, że trójkąt BCD jest szczególny, ponieważ miary jego kątów wynoszą
. Oznacza to, że długość boku znajdującego się naprzeciwko średniego kąta jest o
razy większa od długości boku znajdującego się naprzeciwko najmniejszego kąta, a długość boku znajdującego się naprzeciwko największego kąta jest 2 razy większa od długości najkrótszego boku. Na tej podstawie zapisz długości boków tego trójkąta.
Zapisz stosunek długości boków CD do BD.
Z powstałego równania wyznacz długość boku CD
To kończy dowód.