Na ramionach kąta o wierzchołku A odkładamy dwa odcinki AB i AC, gdzie długość odcinka AB jest równa długości odcinka AC. Następnie odkładamy kolejne dwa odcinki BD i CE, gdzie długość odcinka BD jest równa długości odcinka CE. Odcinki BE i DC przecinają się w punkcie O. Udowodnij, że prosta AO zawiera dwusieczną kąta BAC.
Założenie:
![]()
Teza:
Prosta AO zawiera dwusieczną kąta BAC.
Zadanie:
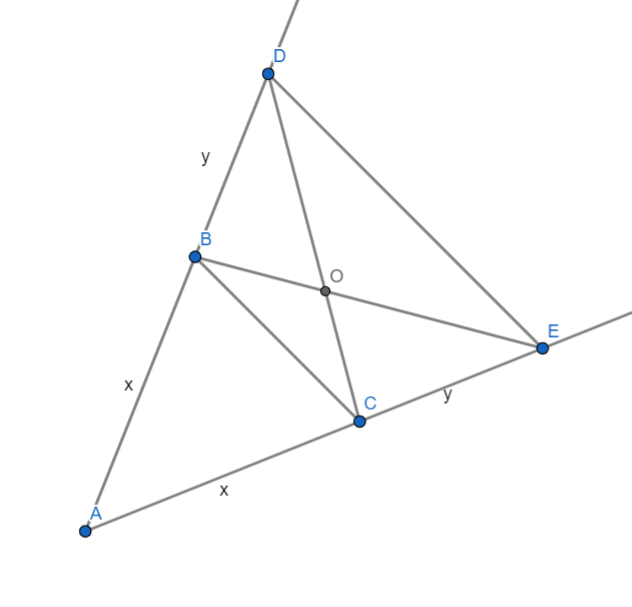
ABC – trójkąt równoramienny.
ADE – trójkąt równoramienny.
Trapez CBDE jest równoramienny.
Przekątne trapezu przecinają się w tym samym stosunku.
![]()
ACOB jest deltoidem.
Dłuższa przekątna tego deltoidu jest również dwusieczną tych kątów.
Prosta AO zawiera dwusieczną kąta BAC.

Zilustruj to.
Zauważ, że:
ABC – trójkąt równoramienny.
ADE – trójkąt równoramienny.
Więc:
Trapez CBDE jest równoramienny.
A co za tym idzie:
Przekątne trapezu przecinają się w tym samym stosunku.
Więc:
![]()
Więc:
ACOB jest deltoidem.
Więc:
Dłuższa przekątna tego deltoidu jest również dwusieczną tych kątów.

Zadanie 7.4.
191Zadanie 7.5.
191Zadanie 7.9.
192Zadanie 7.12.
193Zadanie 7.15.
192Zadanie 7.16.
193Zadanie 7.17.
193Zadanie 7.18.
193Zadanie 7.23.
193Zadanie 7.25.
194Zadanie 7.26.
194Zadanie 7.29.
194Zadanie 7.31.
195Zadanie 7.33.
195Zadanie 7.35.
195Zadanie 7.36.
196Zadanie 7.37.
196Zadanie 7.42.
197Zadanie 7.43.
197Zadanie 7.44.
197Zadanie 7.47.
197Zadanie 7.48.
197Zadanie 7.52.
198Zadanie 7.53.
198Zadanie 7.57.
191Zadanie 7.58.
199Zadanie 7.59.
199Zadanie 7.60.
199Zadanie 7.61.
191Zadanie 7.62.
200Zadanie 7.63.
200Zadanie 7.74.
201Zadanie 7.75.
201Zadanie 7.96.
203Zadanie 7.97.
203Zadanie 7.104.
204Zadanie 7.106.
204Zadanie 7.107.
205Zadanie 7.108.
205Zadanie 7.110.
205Zadanie 7.114.
205Zadanie 7.131.
207Zadanie 7.143.
209Zadanie 7.145.
209Zadanie 7.146.
210Zadanie 7.147.
210Zadanie 7.148.
211Zadanie 7.151.
211Zadanie 7.152.
212Zadanie 7.153.
212Zadanie 7.168.
213Zadanie 7.171.
214Zadanie 7.172.
214Zadanie 7.173.
214Zadanie 7.174.
214Zadanie 25.
218Zadanie 29.
219Zadanie 34.
219Zadanie 38.
220
