Wykaż, że jeżeli długości dwusiecznych CD i C₁D₁ są równe, długości odcinków DA i D₁A₁ są równe, oraz miary kątów CDA i C₁D₁A₁ są równe, to trójkąt ABC jest kongruentny (równoważny) trójkątowi A₁B₁C₁.
Założenie:
![]()
![]()
![]()
Teza:
![]()
Zadanie:
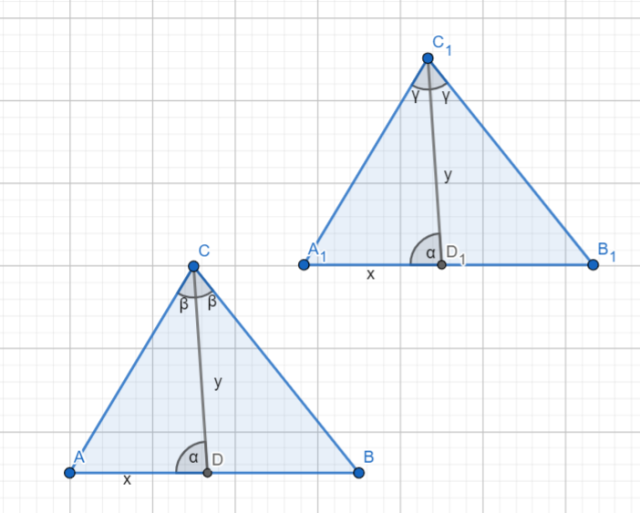
![]()
![]()
![]()
bok – kąt – bok
![]()
![]()
![]()
![]()
![]()
kąt – bok – kąt
![]()

Zwizualizuj dane.
Skoro :
![]()
![]()
![]()
To znaczy, na podstawie zasady bok – kąt – bok , że:
![]()
Więc:
![]()
![]()
![]()
Więc teraz rozważając trójkąt ABC:
![]()
Więc wszystkie kąty w tych trójkątach są takie same i boki odpowiednio AC i ![]()
Na podstawie zasady kąt – bok – kąt:
![]()

Zadanie 7.4.
191Zadanie 7.5.
191Zadanie 7.9.
192Zadanie 7.12.
193Zadanie 7.15.
192Zadanie 7.16.
193Zadanie 7.17.
193Zadanie 7.18.
193Zadanie 7.23.
193Zadanie 7.25.
194Zadanie 7.26.
194Zadanie 7.29.
194Zadanie 7.31.
195Zadanie 7.33.
195Zadanie 7.35.
195Zadanie 7.36.
196Zadanie 7.37.
196Zadanie 7.42.
197Zadanie 7.43.
197Zadanie 7.44.
197Zadanie 7.47.
197Zadanie 7.48.
197Zadanie 7.52.
198Zadanie 7.53.
198Zadanie 7.57.
191Zadanie 7.58.
199Zadanie 7.59.
199Zadanie 7.60.
199Zadanie 7.61.
191Zadanie 7.62.
200Zadanie 7.63.
200Zadanie 7.74.
201Zadanie 7.75.
201Zadanie 7.96.
203Zadanie 7.97.
203Zadanie 7.104.
204Zadanie 7.106.
204Zadanie 7.107.
205Zadanie 7.108.
205Zadanie 7.110.
205Zadanie 7.114.
205Zadanie 7.131.
207Zadanie 7.143.
209Zadanie 7.145.
209Zadanie 7.146.
210Zadanie 7.147.
210Zadanie 7.148.
211Zadanie 7.151.
211Zadanie 7.152.
212Zadanie 7.153.
212Zadanie 7.168.
213Zadanie 7.171.
214Zadanie 7.172.
214Zadanie 7.173.
214Zadanie 7.174.
214Zadanie 25.
218Zadanie 29.
219Zadanie 34.
219Zadanie 38.
220
