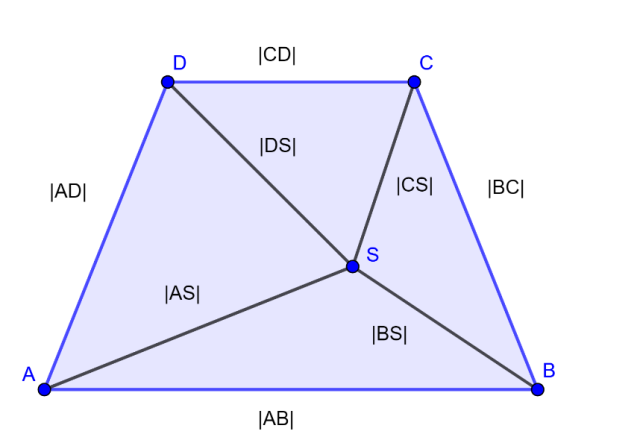
Dany jest czworokąt ABCD oraz dowolny punkt P w płaszczyźnie. Wykaż, że suma odległości punktu P od wierzchołków A, B, C i D jest większa od połowy obwodu tego czworokąta.
Założenie:
Rysunek.
Teza:
![]()
Zadanie:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Zwizualizuj to.
ABCD jest równoległobokiem, czyli:
![]()
Zastosuj twierdzenie o nierówności trójkąta, które mówi, że suma dwóch dowolnych boków trójkąta musi być dłuższa od trzeciego boku.
![]()
![]()
![]()
![]()
Dodaj do siebie nierówności.
![]()
![]()
![]()

Zadanie 7.4.
191Zadanie 7.5.
191Zadanie 7.9.
192Zadanie 7.12.
193Zadanie 7.15.
192Zadanie 7.16.
193Zadanie 7.17.
193Zadanie 7.18.
193Zadanie 7.23.
193Zadanie 7.25.
194Zadanie 7.26.
194Zadanie 7.29.
194Zadanie 7.31.
195Zadanie 7.33.
195Zadanie 7.35.
195Zadanie 7.36.
196Zadanie 7.37.
196Zadanie 7.42.
197Zadanie 7.43.
197Zadanie 7.44.
197Zadanie 7.47.
197Zadanie 7.48.
197Zadanie 7.52.
198Zadanie 7.53.
198Zadanie 7.57.
191Zadanie 7.58.
199Zadanie 7.59.
199Zadanie 7.60.
199Zadanie 7.61.
191Zadanie 7.62.
200Zadanie 7.63.
200Zadanie 7.74.
201Zadanie 7.75.
201Zadanie 7.96.
203Zadanie 7.97.
203Zadanie 7.104.
204Zadanie 7.106.
204Zadanie 7.107.
205Zadanie 7.108.
205Zadanie 7.110.
205Zadanie 7.114.
205Zadanie 7.131.
207Zadanie 7.143.
209Zadanie 7.145.
209Zadanie 7.146.
210Zadanie 7.147.
210Zadanie 7.148.
211Zadanie 7.151.
211Zadanie 7.152.
212Zadanie 7.153.
212Zadanie 7.168.
213Zadanie 7.171.
214Zadanie 7.172.
214Zadanie 7.173.
214Zadanie 7.174.
214Zadanie 25.
218Zadanie 29.
219Zadanie 34.
219Zadanie 38.
220
