Dany jest kąt ostry o wierzchołku O oraz punkt A, który leży na jednym z ramion tego kąta (A≠O). Przez punkt A poprowadzono dwie proste: prostą k, która jest prostopadła do ramienia ![]()
Założenie:
Dany jest kąt ostry o wierzchołku O i punkt A leżący na ramieniu tego kąta, ![]()
![]()
![]()
![]()
![]()
Teza:
![]()
Zadanie:
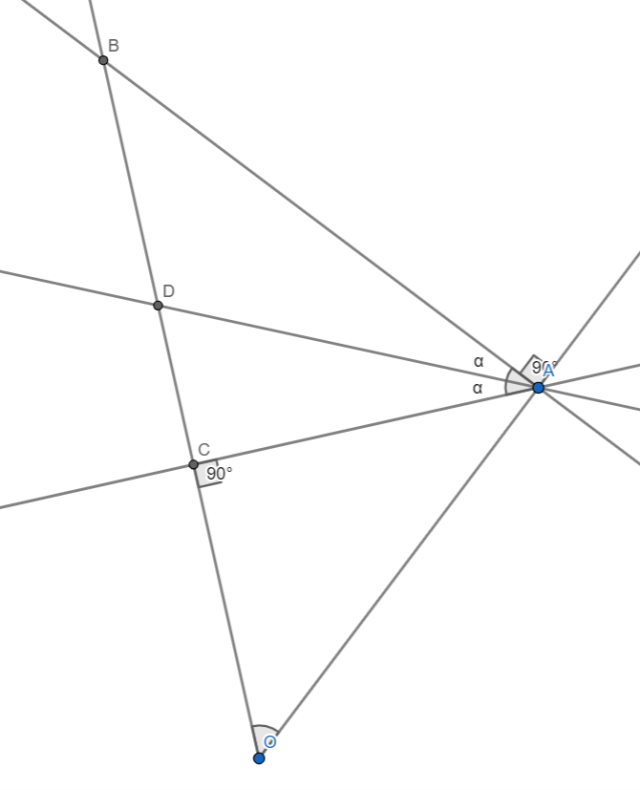
![]()
![]()
![]()
![]()
Trójkąt OAD jest równoramienny, więc ![]()

Zwizualizuj to.
Wypisz widoczne zależności na rysunku.
![]()
Trójkąt AOC:
![]()
![]()
Trójkąt OAD:
![]()
W trójkącie OAD kąty OAD i ODA są sobie równe więc:
Trójkąt OAD jest równoramienny, więc ![]()

Zadanie 7.4.
191Zadanie 7.5.
191Zadanie 7.9.
192Zadanie 7.12.
193Zadanie 7.15.
192Zadanie 7.16.
193Zadanie 7.17.
193Zadanie 7.18.
193Zadanie 7.23.
193Zadanie 7.25.
194Zadanie 7.26.
194Zadanie 7.29.
194Zadanie 7.31.
195Zadanie 7.33.
195Zadanie 7.35.
195Zadanie 7.36.
196Zadanie 7.37.
196Zadanie 7.42.
197Zadanie 7.43.
197Zadanie 7.44.
197Zadanie 7.47.
197Zadanie 7.48.
197Zadanie 7.52.
198Zadanie 7.53.
198Zadanie 7.57.
191Zadanie 7.58.
199Zadanie 7.59.
199Zadanie 7.60.
199Zadanie 7.61.
191Zadanie 7.62.
200Zadanie 7.63.
200Zadanie 7.74.
201Zadanie 7.75.
201Zadanie 7.96.
203Zadanie 7.97.
203Zadanie 7.104.
204Zadanie 7.106.
204Zadanie 7.107.
205Zadanie 7.108.
205Zadanie 7.110.
205Zadanie 7.114.
205Zadanie 7.131.
207Zadanie 7.143.
209Zadanie 7.145.
209Zadanie 7.146.
210Zadanie 7.147.
210Zadanie 7.148.
211Zadanie 7.151.
211Zadanie 7.152.
212Zadanie 7.153.
212Zadanie 7.168.
213Zadanie 7.171.
214Zadanie 7.172.
214Zadanie 7.173.
214Zadanie 7.174.
214Zadanie 25.
218Zadanie 29.
219Zadanie 34.
219Zadanie 38.
220
