Wykaż, że dla dowolnego trójkąta ABC prawdziwa jest podwójna nierówność:
$\text{[math]}$ ,
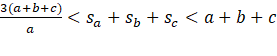
gdzie a, b, c oznaczają długości odpowiednich boków trójkąta, $\text{[math]}$ oznaczają długości środkowych poprowadzonych odpowiednio do boków o długościach a, b, c.

Założenie:

$\text{[math]}$ długości środkowych poprowadzonych odpowiednio do boków o długościach a, b, c

Teza:

$\text{[math]}$

Zadanie:

$\text{[math]}$

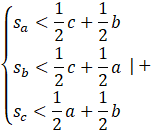
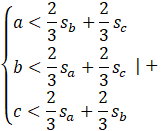
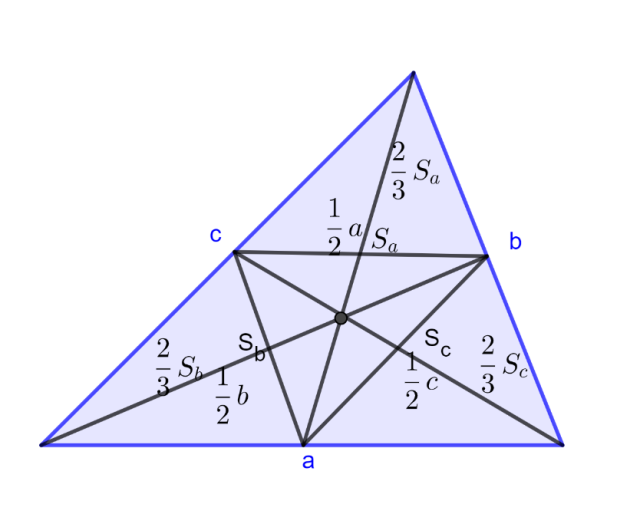
Zwizualizuj dane na rysunku.

Jeśli połączysz środki dwóch dowolnych boków w trójkącie to odcinek, który powstanie będzie miał długość połowy trzeciego boku.

Skorzystaj z twierdzenie o nierówności trójkąta: dla dowolnego trójkąta miara każdego boku musi być mniejsza lub równa sumie miar dwóch pozostałych.

$\text{[math]}$

Utwórz układ równań.

$\text{[math]}$

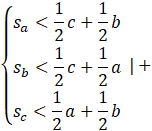
Dodaj wszystkie równania do siebie.

$\text{[math]}$

Skorzystaj o twierdzeniu o środkowych w trójkącie: Trzy środkowe trójkąta przecinają się w jednym punkcie. Punkt ten, nazywany środkiem ciężkości trójkąta, dzieli każdą ze środkowych w stosunku 2:1.

Zapisz równania i stwórz układ równań.

$\text{[math]}$

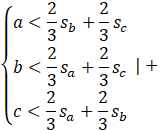
Dodaj wszystkie równania do siebie.

$\text{[math]}$

Zadanie 26., strona 199, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 10, strona 217, NOWA MATeMAtyka 1. Podręcznik. Zakres podstawowy i rozszerzony

Ćwiczenie 23, strona 241, Matematyka i przykłady jej zastosowań. Klasa 1.Podręcznik. Zakres podstawowy i rozszerzony - rozwiązania i odpowiedzi

Zadanie 2.16., strona 382, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6, strona 42, Matematyka z kluczem. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 7.14., strona 102, Prosto do matury 3. Podręcznik do matematyki dla liceum ogólnokształcącego i technikum. Zakres podstawowy

Zadanie wprowadzające 1., strona 222, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 13 zamknięte, strona 97, Matematyka wokół nas. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 5., strona 50, Matematyka. Klasa 5. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 11 zamknięte, strona 41, Matematyka wokół nas. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 7.1.

191

Zadanie 7.2.

191

Zadanie 7.3.

191

Zadanie 7.4.

191

Matematyka. Klasa 1. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 7.130. - strona 207

Zadanie

Wykaż, że dla dowolnego trójkąta ABC prawdziwa jest podwójna nierówność: ,gdzie a, b, c oznaczają długości odpowiednich boków trójkąta, oznaczają długości środkowych poprowadzonych odpowiednio do boków o długościach a, b, c.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania

Wykaż, że dla dowolnego trójkąta ABC prawdziwa jest podwójna nierówność:
$\text{[math]}$ ,
gdzie a, b, c oznaczają długości odpowiednich boków trójkąta, $\text{[math]}$ oznaczają długości środkowych poprowadzonych odpowiednio do boków o długościach a, b, c.