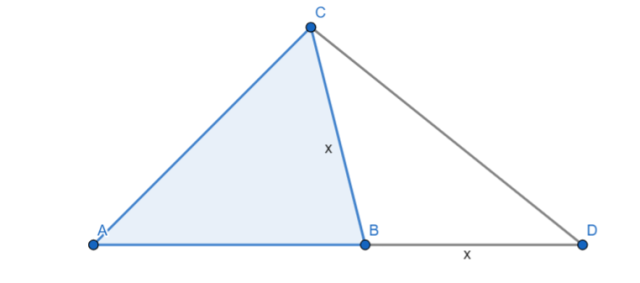
W trójkącie ABC przedłużono bok AB poza wierzchołek B i odłożono odcinek BD, który ma taką samą długość jak odcinek BC. Następnie połączono punkty C i D. Wykaż, że miara kąta CDA jest równa połowie miary kąta CBA.
Założenie:
Teza:
![]()
Zadanie:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Zilustruj to.
Zauważ, że trójkąt BDC jest równoramienny, więc:
![]()
Następnie:
![]()
Teraz kąty na prostej przy punkcie B.
![]()
![]()
![]()
![]()
A teraz zauważ, że:
![]()
Więc:
![]()

Zadanie 7.4.
191Zadanie 7.5.
191Zadanie 7.9.
192Zadanie 7.12.
193Zadanie 7.15.
192Zadanie 7.16.
193Zadanie 7.17.
193Zadanie 7.18.
193Zadanie 7.23.
193Zadanie 7.25.
194Zadanie 7.26.
194Zadanie 7.29.
194Zadanie 7.31.
195Zadanie 7.33.
195Zadanie 7.35.
195Zadanie 7.36.
196Zadanie 7.37.
196Zadanie 7.42.
197Zadanie 7.43.
197Zadanie 7.44.
197Zadanie 7.47.
197Zadanie 7.48.
197Zadanie 7.52.
198Zadanie 7.53.
198Zadanie 7.57.
191Zadanie 7.58.
199Zadanie 7.59.
199Zadanie 7.60.
199Zadanie 7.61.
191Zadanie 7.62.
200Zadanie 7.63.
200Zadanie 7.74.
201Zadanie 7.75.
201Zadanie 7.96.
203Zadanie 7.97.
203Zadanie 7.104.
204Zadanie 7.106.
204Zadanie 7.107.
205Zadanie 7.108.
205Zadanie 7.110.
205Zadanie 7.114.
205Zadanie 7.131.
207Zadanie 7.143.
209Zadanie 7.145.
209Zadanie 7.146.
210Zadanie 7.147.
210Zadanie 7.148.
211Zadanie 7.151.
211Zadanie 7.152.
212Zadanie 7.153.
212Zadanie 7.168.
213Zadanie 7.171.
214Zadanie 7.172.
214Zadanie 7.173.
214Zadanie 7.174.
214Zadanie 25.
218Zadanie 29.
219Zadanie 34.
219Zadanie 38.
220
