![]() – liczb wszystkich możliwych rozkładów kulek
– liczb wszystkich możliwych rozkładów kulek
![]()
Układ A:
![]()
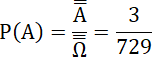
Układ B:
![]()
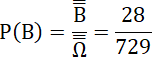
Układ C:
![]()
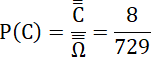
Układ D:
![]()
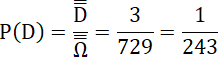
Układ E:
![]()
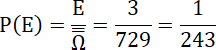
Odpowiedź:
![]()
![]()

Zaważ, że każdym przypadku można rozłożyć 6 rozróżnialnych kulek do trzech pomieszczeń. W takim razie każda z nich ma 3 opcje wyboru, więc liczba wszystkich możliwości wynosi
![]() .
.
Aby określić prawdopodobieństwo
![]() każdego układu oblicz stosunek liczby możliwości tworzących dany układ
każdego układu oblicz stosunek liczby możliwości tworzących dany układ
![]() do wszystkich możliwych rozłożeń kulek
do wszystkich możliwych rozłożeń kulek
![]() .
.
W każdym przypadku zastosuj dwumian Newtona
![]() , gdzie
, gdzie
![]() – określa liczbę kulek, jakie są wybierane, a
– określa liczbę kulek, jakie są wybierane, a
![]() – liczbę kulek, z jakich dokonujemy wyboru.
– liczbę kulek, z jakich dokonujemy wyboru.
Układ A:
Do pierwszej pozycji wkładamy sześć kulek z sześciu możliwych, do drugiej i trzeciej – zero z zeru pozostałych kulek.
Układ B
Do pierwszej pozycji wkładamy dwie kulki z sześciu możliwych, do drugiej – dwie kulki z czterech pozostałych i do trzeciej – dwie z dwóch pozostałych kulek.
Układ C:
Do pierwszej pozycji wkładamy pięć kulek z sześciu możliwych, do drugiej – jedną kulki z jednej pozostałej i do trzeciej – zero z zeru pozostałych kulek.
Układ D:
Do pierwszej pozycji wkładamy dwie kulki z sześciu możliwych, do drugiej – cztery kulki z czterech pozostałych i do trzeciej – zero z zeru pozostałych kulek.
Układ E:
Do pierwszej pozycji wkładamy jedną kulkę z sześciu możliwych, do drugiej – dwie kulki z pięciu pozostałych i do trzeciej – trzy z trzech pozostałych kulek.