Funkcję
przedstaw w postaci kanonicznej, naszkicuj jej wykres i uzupełnij tabelkę.
Własność funkcji
|
|
| Zbiór wartości |
|
| Przedziały monotoniczności | Funkcja rośnie:
Funkcja maleje:
|
| Liczba miejsc zerowych | 2 |
| Równanie osi symetrii wykresu funkcji |
|
Zauważ, że funkcja kwadratowa w postaci kanonicznej wyraża się wzorem:
, gdzie
to współrzędne wierzchołka paraboli.
Liczbę (-10) we wzorze funkcji
zapisz za pomocą sumy liczby (-12) i 2. Wyłącz (-3) przed nawias w trzech pierwszych wyrażeniach, a następnie zauważ wzór skróconego mnożenia na kwadrat różnicy:
.
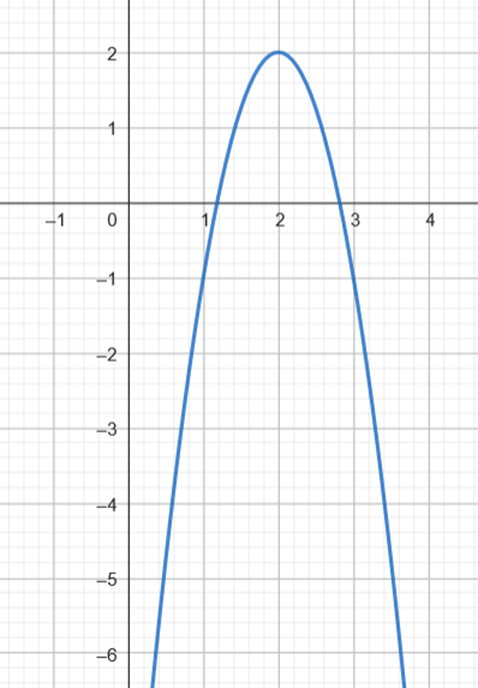
Następnie naszkicuj wykres funkcji
i odczytaj z niego zbiór wartości, czyli przedział, do którego należą wartości funkcji na osi OY, przedziały monotoniczności, czyli argumenty, dla których wykres funkcji
maleje, a dla których rośnie, liczbę miejsc zerowych, czyli przecięcia wykresu z osią OX oraz równanie symetrii wykresu funkcji, czyli równanie prostej
przechodzącej przez wierzchołek paraboli.