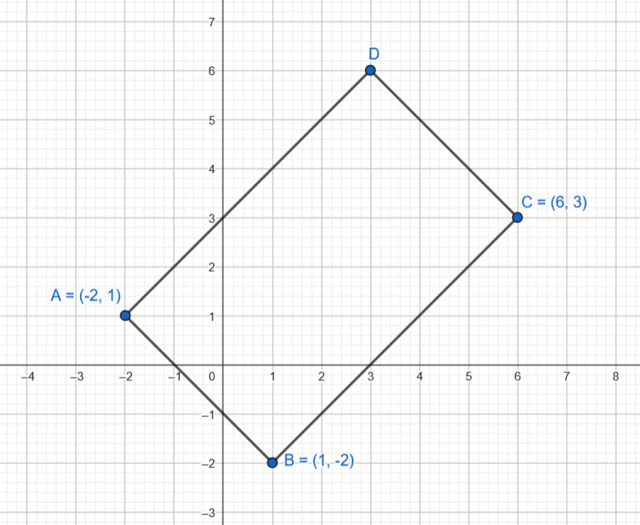
Wyznacz równania prostych zawierających boki prostokąta ABCD, jeśli A(-2,1), B(1,-2), C(6,3).

Prosta AB:

$\text{[math]}$

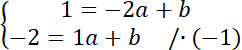
Prosta BC:

$\text{[math]}$

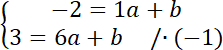
Prosta AD jest prostopadła do prostej AB:

$\text{[math]}$

Prosta CD jest prostopadła do prostej BC:

$\text{[math]}$

Wykonaj rysunek pomocniczy.

Współrzędne punktów A i B podstaw pod równanie kierunkowe prostej: $\text{[math]}$ . Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Całe drugie równanie pomnóż przez -1, aby współczynniki przy $\text{[math]}$ były przeciwne, a następnie wyznacz wartość współczynnika $\text{[math]}$ dodając je do siebie stronami.

Podstaw wyznaczoną wartość $\text{[math]}$ pod jedno z początkowych równań i na tej podstawie wyznacz wartość współczynnika $\text{[math]}$ .

W podobny sposób wyznacz równanie prostej BC.

Skorzystaj z tego, że sąsiednie boki w prostokącie są prostopadłe, więc proste AB i AD oraz BC i CD będą względem siebie prostopadłe. Dodatkowo zauważ, że jeśli dwie proste mają być prostopadłe, to ich współczynniki kierunkowe muszą być przeciwne i odwrotne, czyli spełniać warunek: $\text{[math]}$ .

Pod powyższe równanie podstaw współczynnik kierunkowy prostej AB i wyznacz wartość współczynnika prostej AD do niej prostopadłej.

Skorzystaj z tego, że do wykresu szukanej funkcji należy punkt A. Podstaw jego współrzędne w miejsce $\text{[math]}$ i $\text{[math]}$ w równaniu kierunkowym prostej, aby obliczyć wartość współczynnika $\text{[math]}$ .