Oblicz pole czworokąta ABCD, jeśli prosta
![]() przecina osie układu współrzędnych w punktach A i B, a prosta
przecina osie układu współrzędnych w punktach A i B, a prosta
![]() – w punktach C i D
– w punktach C i D
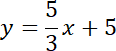
Przecięcie z osią OY:
![]()
Przecięcia z osią OX:
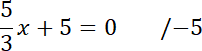
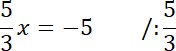
![]()
![]()
![]()
Przecięcie z osią OY:
![]()
Przecięcia z osią OX:
![]()
![]()
![]()
![]()
![]()
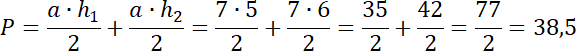

Zauważ, że współczynnik
![]() decyduje o miejscu przecięcia wykresu z osią OY. Więc druga współrzędna jego punktu jest jednocześnie wartością tego współczynnika.
decyduje o miejscu przecięcia wykresu z osią OY. Więc druga współrzędna jego punktu jest jednocześnie wartością tego współczynnika.
Zaś aby wyznaczyć przecięcie funkcji z osią OX w miejsce
![]() we wzorze funkcji musisz wstawić 0 i wyznaczyć
we wzorze funkcji musisz wstawić 0 i wyznaczyć
![]() z powstałego równania.
z powstałego równania.
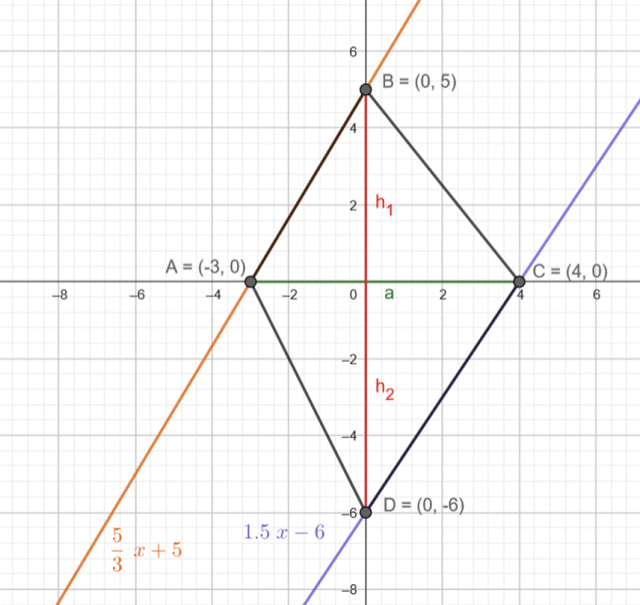
Na tej podstawie oblicz współrzędne przecięcia wykresów prostych podanych w treści zadania z osiami układu współrzędnych.
Zauważ, że powstała figura składa się z dwóch trójkątów o takiej samej podstawie. Oblicz więc sumę ich pól, ale obliczyć pole powstałej figury.

Ćwiczenie 1
201Ćwiczenie 2
202Ćwiczenie 3
202Ćwiczenie 5
203Zadanie 1
203Zadanie 2
203Zadanie 4
203Zadanie 5
204Zadanie 8
204Zadanie 9
204Zadanie 11
204Zadanie 12
204Ćwiczenie 1
205Ćwiczenie 2
205Ćwiczenie 3
206Ćwiczenie 4
206Ćwiczenie 5
206Zadanie 2
207Zadanie 3
207Zadanie 4
207Zadanie 5
207Zadanie 6
207Ćwiczenie 2
208Ćwiczenie 3
208Ćwiczenie 4
208Ćwiczenie 6
210Ćwiczenie 7
210Ćwiczenie 8
210Ćwiczenie 9
210Ćwiczenie 10
211Zadanie 1
211Zadanie 2
211Zadanie 3
211Zadanie 4
211Zadanie 5
211Zadanie 6
211Zadanie 7
212Zadanie 8
212Zadanie 9
212Zadanie 11
212Zadanie 12
212Zadanie 13
212Ćwiczenie 1
213Ćwiczenie 2
214Ćwiczenie 3
214Ćwiczenie 4
214Ćwiczenie 5
215Ćwiczenie 7
215Zadanie 1
215Zadanie 2
216Zadanie 3
216Zadanie 4
216Zadanie 6
216Ćwiczenie 1
217Ćwiczenie 2
217Ćwiczenie 4
218Ćwiczenie 5
218Ćwiczenie 6
219Ćwiczenie 7
219Ćwiczenie 8
219Ćwiczenie 9
219Zadanie 3
220Zadanie 4
220Zadanie 5
220Zadanie 6
220Zadanie 7
220Ćwiczenie 1
222Ćwiczenie 2
223Ćwiczenie 3
223Ćwiczenie 5
223Ćwiczenie 6
224Ćwiczenie 7
224Zadanie 1
224Zadanie 2
224Zadanie 3
224Zadanie 4
225Zadanie 5
225Zadanie 7
225Zadanie 8
225Zadanie 9
225Zadanie 10
225Zadanie 1
226Zadanie 2
226Zadanie 3
226Zadanie 4
226Ćwiczenie 1
227Ćwiczenie 2
228Ćwiczenie 3
228Zadanie 1
229Zadanie 2
229Zadanie 3
229Zadanie 4
229Zadanie 5
229Zadanie 7
230Zadanie 8
230Zadanie 9
230Zadanie 10
230Zadanie 11
230Ćwiczenie 2
231Zadanie 1
232Zadanie 2
232Zadanie 3
233Zadanie 4
233Zadanie 5
233Zadanie 1
234Zadanie 2
234Zadanie 3
234Zadanie 4
234Zadanie 5
234Zadanie 6
234Zadanie 7
234Zadanie 8
234Zadanie 9
234Zadanie 1
235Zadanie 2
235Zadanie 4
235Zadanie 5
235Zadanie 7
235
