W tym zadaniu należy określić ilość rozwiązań równania w zależności od parametru m i naszkicować wykres funkcji
.
Rozpatrujemy trzy przedziały:
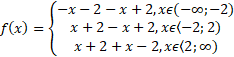
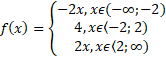
0 rozwiązań:
2 rozwiązania:
Nieskończenie wiele rozwiązań:
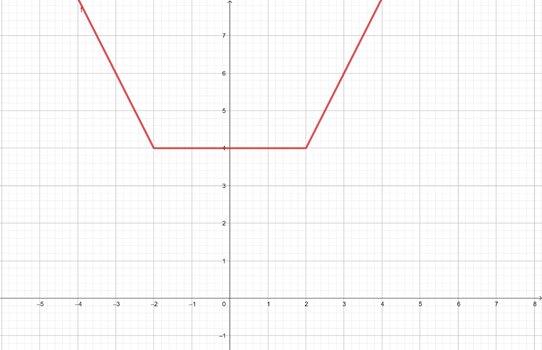
Naszkicuj wykres w trzech przedziałach. Sprawdź, dla jakich argumentów x zerują się wartości bezwzględne – te wartości określą przedziały, w jakich będziemy rozpatrywać funkcję. Po naszkicowaniu wykresu oś OY jest równoznaczna z osią OM. Zastanów się, dla jakich wartości na osi OM wykres funkcji nie ma żadnych rozwiązań, gdzie ma tylko jedno rozwiązanie, a gdzie ma ich nieskończenie wiele. Wykres ma nieskończenie wiele rozwiązań, jeśli funkcja jest ciągła, czyli przyjmuje tę samą wartość dla nieskończonej liczby argumentów na osi OX. Jeśli funkcja przyjmuje tę samą wartość dla dokładnie dwóch różnych argumentów x, to oznacza, że w tym miejscu/ przedziale funkcja ma dwa rozwiązania.