W tym zadaniu należy znaleźć wzory funkcji, które ograniczają trójkąt o polu 12. Wykresy tych funkcji przecinają się w punkcie
.
– wzór ogólny funkcji liniowej
– długość podstawy trójkąta, czyli odległość między miejscami 0wymi na osi OX
Miejsca zerowe to liczby przeciwne, więc będą to punkty
i
Wzór funkcji I, punkty:
i
i
Wzór funkcji II, punkty:
i
i
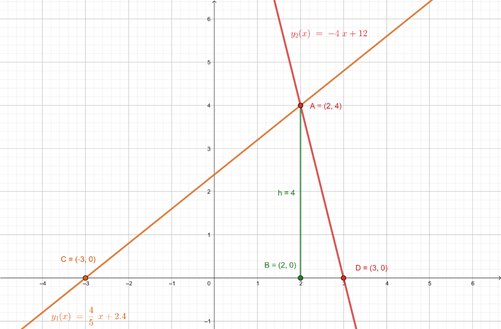
Odpowiedź: Wzory funkcji to
i
.
Zauważ, że punkt
jest wierzchołkiem trójkąta. Jego wysokość wynosi tyle, co wartość rzędnej 4. Oblicz długość podstawy. Z treści zadania wiemy, że miejsca zerowe na osi OX są liczbami przeciwnymi. Jedyne liczby spełniające zadnie to
i
– pamiętaj, że podstawa trójkąta musi mieć długość 6. Teraz sporządź rysunek pomocniczy i narysuj dwie funkcje przechodzące przez wyznaczone punkty. Zapisz dwa układy równań, po jednym dla każdej szukanej funkcji. Oblicz wartości współczynników kierunkowych i przesunięć na osi OY. Zapisz wzory tych funkcji.