W tym zadaniu musisz obliczyć pole ścian opisanego w zadaniu ostrosłupa.
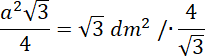
![]()
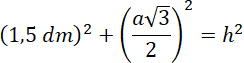
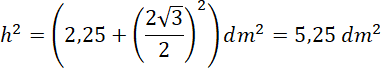
![]()
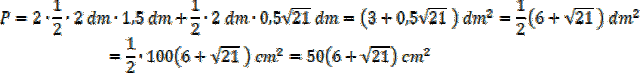

Podstawą ostrosłupa jest trójkąt równoboczny o polu
![]() .
.
Policz długość krawędzi podstawy, korzystając ze wzoru na pole trójkąta równobocznego:
![]()
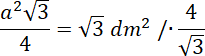
![]()
Jedna z krawędzi bocznych o długości 15 cm jest prostopadła do podstawy. Dwie ściany boczne to zatem trójkąty o wysokości 1,5 dm i podstawie 2 dm. Wysokość ostatniej ściany bocznej policz z twierdzenia Pitagorasa jako przeciwprostokątną trójkąta prostokątnego utworzonego przez wysokość podstawy i wysokość ostrosłupa:
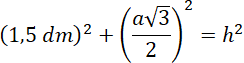
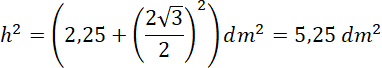
![]()
Policz pole trzech ścian bocznych:
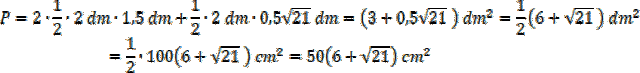

Zadanie 3.
63Zadanie 4.
63Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Zadanie 11.
64Zadanie 3.
65Zadanie 13.
66Zadanie 20.
67Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 5.
68Zadanie 7.
69Zadanie 9.
69Zadanie 17.
70Zadanie 1.
70Zadanie 2.
70Zadanie 3.
70Zadanie 7.
72Zadanie 10.
72Zadanie 2.
75Zadanie 3.
75Zadanie 4.
75Zadanie 5.
75Zadanie 6.
75
