W tym zadaniu musisz obliczyć pole powierzchni ścian opisanego ostrosłupa.
![]()
![]()
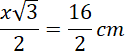
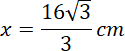
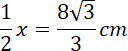
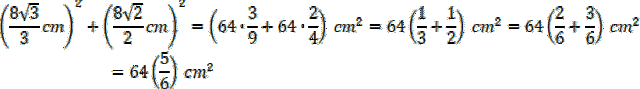
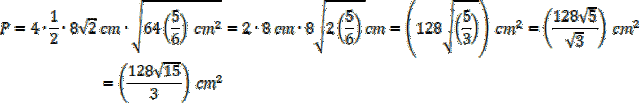

Przekrój ostrosłupa prawidłowego czworokątnego, zawierający dwie krawędzie boczne i przekątną podstawy, jest trójkątem równoramiennym, w którym miara kąta przy podstawie jest równa
![]() , a długość podstawy wynosi 16 cm – to znaczy, że przekątna kwadratu w podstawie ostrosłupa ma 16 cm. Policz długość krawędzi podstawy:
, a długość podstawy wynosi 16 cm – to znaczy, że przekątna kwadratu w podstawie ostrosłupa ma 16 cm. Policz długość krawędzi podstawy:
![]()
![]()
Policz wysokość ostrosłupa korzystając z własności trójkąta
![]() . Połowa przekątnej to wysokość tego trójkąta, natomiast wysokość ostrosłupa to
. Połowa przekątnej to wysokość tego trójkąta, natomiast wysokość ostrosłupa to
![]()
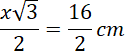
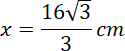
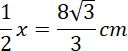
Następnie możesz obliczyć wysokość ściany bocznej, korzystając z twierdzenia Pitagorasa:
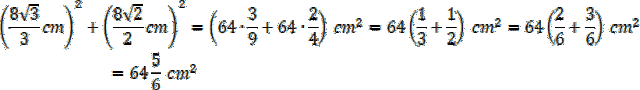
Oblicz pole powierzchni bocznej, czyli pole 4 identycznych ścian:
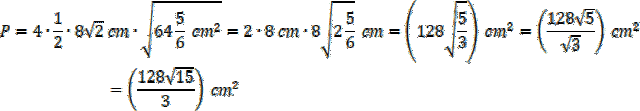

Zadanie 3.
63Zadanie 4.
63Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Zadanie 11.
64Zadanie 3.
65Zadanie 13.
66Zadanie 20.
67Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 5.
68Zadanie 7.
69Zadanie 9.
69Zadanie 17.
70Zadanie 1.
70Zadanie 2.
70Zadanie 3.
70Zadanie 7.
72Zadanie 10.
72Zadanie 2.
75Zadanie 3.
75Zadanie 4.
75Zadanie 5.
75Zadanie 6.
75
