W tym zadaniu musisz obliczyć pole powierzchni całkowitej oraz sumę długości wszystkich krawędzi ostrosłupa opisanego w zadaniu.
![]()
![]()
![]()
![]()
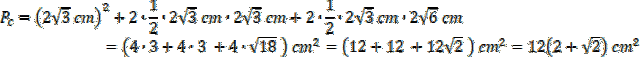

Ten ostrosłup ma w podstawie kwadrat, którego pole to
![]() . Policz długość krawędzi podstawy:
. Policz długość krawędzi podstawy:
![]()
Jedna z krawędzi bocznych, prostopadła do płaszczyzny podstawy, ma długość równą długości krawędzi podstawy, to znaczy, że dwie ściany to trójkąty prostokątne równoramienne. Oblicz długość przeciwprostokątnej:
![]()
Aby policzyć sumę wszystkich krawędzi, potrzebujesz jeszcze najdłuższej krawędzi bocznej, która jest przeciwprostokątną trójkąta tworzonego przez przekątną podstawy i wysokość ostrosłupa. Oblicz długość tej krawędzi z twierdzenia Pitagorasa:
![]()
Ta krawędź będzie mieć 6 cm. Policz sumę długości wszystkich krawędzi – pamiętaj, że w ostrosłupie o podstawie kwadratu są cztery krawędzie podstawy i cztery krawędzie boczne.
![]()
Teraz Oblicz pole powierzchni całkowitej, czyli pole kwadratu w podstawie oraz pole czterech ścian. Dwie ściany boczne to trójkąty prostokątne o podstawie
![]() i takiej samej wysokości
i takiej samej wysokości
![]() , dwie kolejne ściany również są trójkątami prostokątnymi o podstawie
, dwie kolejne ściany również są trójkątami prostokątnymi o podstawie
![]() i wysokości równej
i wysokości równej
![]() – przeciwprostokątnej poprzedniego trójkąta.
– przeciwprostokątnej poprzedniego trójkąta.
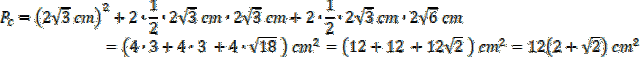

Zadanie 3.
63Zadanie 4.
63Zadanie 6.
64Zadanie 7.
64Zadanie 8.
64Zadanie 11.
64Zadanie 3.
65Zadanie 13.
66Zadanie 20.
67Zadanie 1.
68Zadanie 2.
68Zadanie 3.
68Zadanie 4.
68Zadanie 5.
68Zadanie 7.
69Zadanie 9.
69Zadanie 17.
70Zadanie 1.
70Zadanie 2.
70Zadanie 3.
70Zadanie 7.
72Zadanie 10.
72Zadanie 2.
75Zadanie 3.
75Zadanie 4.
75Zadanie 5.
75Zadanie 6.
75
