W tym zadaniu określ, czy trójkąt o długościach boków 5, 7, 9 jest ostrokątny, prostokątny czy rozwartokątny.
92 = 52 + 72 – 2 ∙ 5 ∙ 7 ∙ cos γ
81 = 25 + 49 – 70 ∙ cos γ
81 = 74 - 70 ∙ cos γ / - 74
7 = -70 ∙ cos γ / : 70
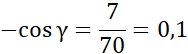
-cos 84˚ = cos (180˚ - 84˚) = cos 96˚
![]()
Największy kąt tego trójkąta to 96˚, więc trójkąt jest rozwartokątny.

Największy bok trójkąta leży naprzeciwko jego najdłuższego boku. Aby wyznaczyć największy kąt tego trójkąta skorzystaj z twierdzenia cosinusów a2 = b2 + c2 – 2bc ∙ cos α, gdzie b i c to sąsiednie boki trójkąta, α to kąt między nimi, natomiast a to bok naprzeciwko kąta α.
92 = 52 + 72 – 2 ∙ 5 ∙ 7 ∙ cos γ
81 = 25 + 49 – 70 ∙ cos γ
81 = 74 - 70 ∙ cos γ / - 74
7 = -70 ∙ cos γ / : 70
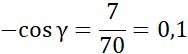
Odczytaj wartość cos α = 0,1 z tabeli na stronie 249.
Skorzystaj z równości cos(180˚ - α) = -cos α.
-cos 84˚ = cos (180˚ - 84˚) = cos 96˚
![]()

Ćwiczenie A
164Ćwiczenie B
165Ćwiczenie D
166Zadanie 1
166Zadanie 2
167Zadanie 3
167Zadanie 4
167Zadanie 7
166Zadanie 8
166Zadanie 11
168Zadanie 12
168Ćwiczenie C
170Ćwiczenie D
171Zadanie 2
171Zadanie 3
172Zadanie 5
172Zadanie 6
172Zadanie 7
172Zadanie 9
173Zadanie 11
173Zadanie 12
173Zadanie 13
173Zadanie 1
177Zadanie 3
177Zadanie 4
177Zadanie 5
178Zadanie 10
178Zadanie 13
178Zadanie 14
178Zadanie 15
179Zadanie 19
179Zadanie 20
179Zadanie 4
182Zadanie 10
183Zadanie 11
184Zadanie 12
184Zadanie 1
186Zadanie 2
186Zadanie 3
187Zadanie 4
186Przykład 1
189Zadanie 1
190Zadanie 3
190Zadanie 4
190Zadanie 5
190Zadanie 6
190Zadanie 7
190Zadanie 8
190Zadanie 9
190Zadanie 10
191Ćwiczenie B
192Przykład 2
194Przykład 3
194Zadanie 1
196Zadanie 3
196Zadanie 4
196Zadanie 5
196Zadanie 6
196Zadanie 7
197Zadanie 8
197Zadanie 9
197Zadanie 11
197Zadanie 12
197Zadanie 13
197Zadanie 14
198Zadanie 15
198Zadanie 16
198Zadanie 1
202Zadanie 2
202Zadanie 4
202Zadanie 5
203Zadanie 6
203Zadanie 7
203Zadanie 8
203Zadanie 11
203Zadanie 1
207Zadanie 2
207Zadanie 3
207Zadanie 12
210Zadanie 13
210
