W tym zadaniu musisz udowodnić, że kąty ostre trapezu mają podaną miarę.
Założenie:
Przekątna AC tworzy z ramieniem BC kąt prosty i jest jednocześnie dwusieczną kąta przy wierzchołku A.
Teza:
|DC| = |2|AB|
Dowód:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Narysuj trapez.
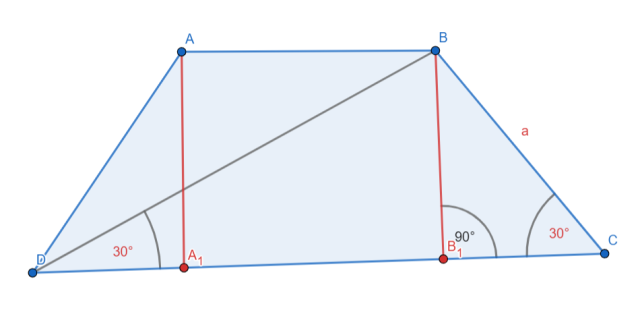
![]()
![]()
Zauważ, że trójkąt BB’C jest trójkątem szczególnym i trójkąt DCB też – oba o kątach ![]()
![]()
![]()
![]()
Teraz dodaj poszczególne elementy, z których składa się bok CD.
![]()
![]()
![]()
![]()
![]()
![]()

Zadanie 4.1.
63Zadanie 4.2.
63Zadanie 4.6.
64Zadanie 4.8.
64Zadanie 4.9.
64Zadanie 4.10.
64Zadanie 4.14.
65Zadanie 4.15.
65Zadanie 4.16.
65Zadanie 4.21.
66Zadanie 4.22.
66Zadanie 4.23.
66Zadanie 4.24.
66Zadanie 4.25.
66Zadanie 4.27.
66Zadanie 4.29.
67Zadanie 4.30.
67Zadanie 4.32.
67Zadanie 4.36.
68Zadanie 4.38.
68Zadanie 4.40.
68Zadanie 4.44.
69Zadanie 4.49.
69Zadanie 4.50.
69Zadanie 4.56.
70Zadanie 4.58.
70Zadanie 4.60.
70Zadanie 4.62
70Zadanie 4.64.
70Zadanie 4.69.
71Zadanie 4.70.
71Zadanie 4.71.
71Zadanie 4.75.
72Zadanie 4.76.
72Zadanie 4.77.
73Zadanie 4.78.
73Zadanie 4.79.
73Zadanie 4.80.
73Zadanie 4.82.
74Zadanie 4.88.
74
