Oblicz wartości dwóch najmniejszych grubości błonki mydlanej (n = 1,33), dla których zachodzi interferencja konstruktywna promieni światła barwy zielonej o długości λ = 548 nm odbitych od dwóch powierzchni błonki.
DANE:
![]()
![]()
![]()
SZUKANE:
![]()
![]()
WZÓR:
Wyznaczamy grubości błonek bańki mydlanej:
![]()
![]()
![]()
Prawo Snelliusa:
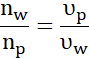
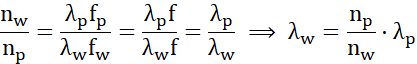
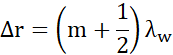
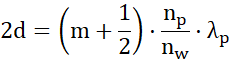
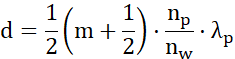
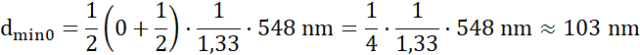
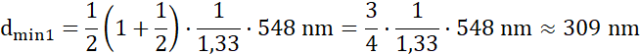
Odpowiedź: C. 103 nm, 309 nm

Przyjęte oznaczenia:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Najpierw skorzystaj z prawa Snelliusa (załamania światła) i wyznacz długość fali w wodzie w zależności od jej długości w powietrzu (dla którego współczynnik załamania wynosi 1). Skorzystaj z faktu, że podczas zmiany ośrodka nie dochodzi do zmiany częstotliwości.
Zauważ, że skoro dochodzi do konstruktywnej interferencji promieni odbitych, to oznacza, że dochodzi do wygaszenia promieni padających, czyli zachodzi relacja ![]()
Wyznacz z równania szukaną grubość, a następnie podstaw dane.

Zadanie 16.1.9.
16Zadanie 16.1.15.
17Zadanie 16.2.7.
25Zadanie 16.2.12.
26Zadanie 16.2.16.
27Zadanie 16.3.1.
36Zadanie 16.3.9.
37Zadanie 16.3.13.
38Zadanie 16.3.14.
38Zadanie 16.3.15.
39Zadanie 16.3.17.
40Zadanie 16.5.5.
53Zadanie 16.5.7.
53Zadanie 16.6.3.
59Zadanie 16.6.6.
60Zadanie 16.6.13.
62Zadanie 16.7.1.
66Zadanie 16.7.4.
66Zadanie 16.7.6.
67Zadanie 16.7.9.
68Zadanie 16.7.10.
68Zadanie 16.8.2.
77Zadanie 16.8.3.
78Zadanie 16.8.4.
78Zadanie 16.8.5.
79Zadanie 16.8.9.
80Zadanie 16.8.10.
80Zadanie 16.8.11.
80Zadanie 16.8.12.
80Zadanie 16.8.15.
81Zadanie 16.8.20.
81Zadanie 16.8.21.
81Zadanie 16.8.23.
82Zadanie 16.9.10.
92Zadanie 16.10.14.
103Zadanie 16.12.1.
115Zadanie 16.12.8.
117Zadanie 4.
122Zadanie 5.
122Zadanie 6.
123Zadanie 7.
123
